ترجمههای کامران بزرگزاد

زندگی و کارهای ریاضیدانان نامی جهان
این چهارمین کتابی است که از یان استوارت به فارسی ترجمه میکنم. سه کتاب قبلی عبارت بودند از چرا زیبایی واقعیت است؟، جهان شگفت انگیز اعداد، و مقدمهای بسیار کوتاه درباره بینهایت. تمرکز کتاب حاضر بر روی زندگی و کارهای ریاضیدانان نامی جهان از هزاره سوم پیش از میلاد، تا پایان قرن بیستم است. کتاب صرفاً جنبه تاریخی ندارد و ناگزیر به مفاهیمی اشاره میکند که ریاضیدانان در تکامل آنها نقش داشتهاند. البته واضح است که با حجم اندک این کتاب حتی نمیتوان به ریاضیدانان نامی یک قاره یا یک کشور هم اشاره کرد، چه رسد ریاضیدانان جهان. بنابراین باید راه غربالگری پیشه ساخت و آنهایی را شامل کرد که اسطوره هستند و حقیقتاً معروفیت جهانی دارند، و این کاریست که استوارت در تدوین این کتاب انجام داده.
این کتاب میتواند برای کلیه کسانی که به تاریخ علم، و عليالخصوص ریاضیات،
علاقه دارند جالب و خواندنی باشد. خواندن کتاب هیچ پیش نیازی ندارد و همه افراد میتوانند
از آن بهره بگیرند.
یان استوارت ریاضیدان و مؤلف انگلیسی در سال 1945 در انگلستان بدنیا
آمد، مدرک کارشناسی خود را در رشته ریاضی از دانشگاه کمبریج دریافت کرد، سپس در
سال 1967 برای گرفتن دکترای خود به دانشگاه وارویک (Warwick) رفت، و از آن پس نیز در همین دانشگاه مشغول تدریس و تحقیق بوده
است.
استوارت از جمله نویسندگانی است که به ترویج دانش علمی، و بالاخص ریاضیات،
شهرت دارد. از وی بیش 10 کتاب درسی، 30 کتاب عمومی غیر تخصصی، و بیش از صد و پنجاه
مقاله منتشر شده. سری کتابهای (Discworld)، که او با زیست شناس مشهور جک کوهن نوشته بسیار معروف و
پر فروش هستند.
کامران بزرگزاد
پاییز 1399
مبداء کلیه شاخههای علوم را میتوان در پشت ابرهای تاریخ پیدا کرد، ولی آنچه
که بعدها تاریخ در اکثر موضوعات به ما میگوید نتیجهگیریهایی شبیه این هستند:
’حالا ما میدانیم که این مورد دیگر صحیح نیست‘، یا ’این مورد در مسیر درستی قرار
داشت، ولی دیدگاه امروز با گذشته فرق دارند‘. مثلاً ارسطو فیلسوف یونانی عقیده
داشت که یک اسب مسابقه هیچ وقت بطور کامل در هوا معلق نمیماند، چیزی که در سال
1878 توسط عکاس انگلیسی ادوارد مایبریج (Eadweard Muybridge) با استفاده
از قرار دادن چندین دوربین در کنار زمین مسابقه رد شد. نظریههای ارسطو درباره
حرکت نیز بطور کامل توسط کسانی مانند گالیله و نیوتون رد شدند، و نظرات او درباره
ذهن نیز هیچ ارتباط مفیدی با علوم اعصاب و روانشناسی مدرن ندارند.
در میان شاخههای علم، وضعیت ریاضیات متفاوت است. نتایج این علم ماندگارند.
هنگامی که بابلیان باستان در حدود 2000 سال پیش از میلاد راهحلی برای حل معادلات
درجه دوم پیدا کردند، بدلیل اینکه این راهحل صحیح بود هیچگاه منسوخ نشد و آنها
این را میدانستند. بعد از گذشت 4000 سال، هنوز هم این راهحل صحیح است. ما امروزه
نتایج را بصورت فرمول بیان میکنیم، ولی استدلال یکی است. خط پیوستهای از تفکر
ریاضی وجود دارد که از فردا تا زمان بابلیان امتداد دارد. هنگامی که ارشمیدس فهمید چگونه حجم کره را محاسبه
کند، او از علائم جبری استفاده نمیکرد، و به آن شکلی که ما امروز از عددی بنام π استفاده میکنیم، او اینکار را انجام نمیداد. او نتایج را بشکل
هندسی، و بصورت نسبتها بیان میکرد. این همان کاری بود که آن زمان یونانیان انجام
میداد. هرچند جوابی که او بدست آورده بود فوراً قابلتشخیص است و میتوان فهمید
که معادل فرمول ![]() πr2 امروزی است.
πr2 امروزی است.
راستش را بخواهید، حقیقتاً تعداد اندکی از کشفیات غیر ریاضی هستند که از دنیای
باستان به ما رسیده و اینقدر پابرجا بودهاند. اصل جابجایی ارشمیدس و قانون اهرمها
نمونههایی از این موارد هستند. برخی از اصول فیزیک و مهندسی یونان باستان هنوز هم
پابرجا هستند. ولی ماندگاری آنها جزء موارد استثنا است، درحالی که آنچه از ریاضیات
بجا مانده، به قاعده نزدیک است. کتاب اصول اقلیدس، که پایههای منطقی هندسه را بنا
نهاد، هنوز هم مورد مطالعه قرار میگیرد. قضایای این کتاب هنوز هم صحیح هستند، و
بسیاری از آنها مفید باقی ماندهاند. ما در ریاضیات به حرکت خودمان ادامه میدهیم،
ولی تاریخ را هم فراموش نمیکنیم.
لازم است پیش از ادامه کتاب به دو موضوع اشاره کنم. یکی اینکه اهمیت یک روش یا
یک قضیه میتواند تغییر کند. همانطور که سرحدات ریاضیات جابجا شدهاند یا تکنیکهای
جدیدی یافت شدهاند، بسیاری از حوزههای این علم نیز ناگهان از مُد افتاده یا
منسوخ شدهاند. ولی آنها هنوز هم صحیح هستند، و هر از چندگاهی، معمولاً
بدلیل اینکه کشفیات تازهای در رابطه با حوزههای دیگر، یک کاربرد جدید، یا پیشرفت
مهمی در روشها بوجود آمده، آن حوزه منسوخ دوباره احیا شده. مورد دوم این است که
ریاضیدانان نه فقط حرکت میکنند، بلکه موضوعاتِ خودشان را توسعه میدهند؛ آنها
همچنین مقدار عظیمی از ریاضیاتِ جدید، مهم، زیبا، و مفید را تولید میکنند.
نکته اصلی که در اینجا بیان شد این است که هنگامی که یک قضیه ریاضی بصورت صحیح
اثبات شد، این برای همیشه به چیزی تبدیل خواهد شد که ما میتوانیم بر اساس آن
چیزهایی را بنا کنیم. حتی اگر مفهوم اثبات نسبت به زمان اقلیدس برای ما بسیار سختتر
شده باشد، ما میتوانیم آنچه را حالا بعنوان شکاف میبینیم پر کنیم، و نتایج قبلی
هنوز پابرجا خواهند بود.
![]()
کتاب چهرههای برجسته جهان ریاضیات جنبههایی از روندهای عارفانهای را
بررسی میکند که ریاضیاتِ جدید را بوجود آورده است. ریاضیات در خلاء بوجود نمیآید،
بلکه توسط انسانها خلق میشود. برخی از این انسانها نبوغی اصیل و ذهنی روشن
دارند، کسانی که با پیشرفتهای مهم وابستهاند، اینها همان پیشگامانی هستند که ما
از آنها بنام چهرههای برجسته یاد کردهایم. تاریخنگاران به درستی اذعان میکنند
که کارهای بزرگ همیشه به پشتیبانی و همکاریهای گستردهای وابستهاند که از سوی
افراد مختلف انجام میشود. سئوالات مهم یا پربار میتواند توسط مجهولات وابسته
بیان شوند؛ ایدههای مهم بسختی میتوانند توسط کسانی که فاقد تواناییهای فنی
هستند درک شده و به دیدگاهها و روشهای جدید تبدیل شوند. نیوتون گفته بود ”من بر
شانه غولها ایستادهام“.
به هر حال غولهایی هستند که مسیر را مشخص میکنند و بقیه ما آنها را دنبال میکنیم.
از طریق بررسی سرگذشت و آثار تعدادی از اشخاص برجسته ما میتوانیم بفهمیم که
ریاضیات جدید چگونه بوجود میآید، چه کسی آن را ایجاد کرده، و ریاضیدانان
چگونه زندگی میکردهاند. من به این اشخاص تنها به عنوان پیشگامانی که راه را به
ما نشان دادهاند نمینگرم، بلکه آنها را راهگشایانی میبینم که مسیر ناهموار
جنگلِ ریاضی را برای ما صاف کردهاند. آنها بیشتر وقت خودشان را صرف کندن خارهای
موجود در مسیر، یا عبور از باتلاقها کردهاند، ولی هر از چندگاهی هم به سرزمینهای
ثروتمندی رسیدهاند که مملو از جواهرات پنهان هستند. آنها به مناطقی از ذهن نفوذ
کردهاند که پیش از این برای بشر ناشناخته بوده.
درواقع آنها این مناطق را خودشان ساختهاند. جنگلِ ریاضی شبیه جنگلهای
بارانی آمازون یا کنگو نیست. یک پیشگامِ ریاضی شبیه کسی مثل دیوید لیوینستون نیست
که بدنبال سرچشمه رود نیل باشد. لیوینگستون چیزهایی را ’کشف میکرد‘ که از قبل
وجود داشتند. به ویژه، اهالی بومی میدانستند آنها وجود دارند. ولی در آن
روزها اروپاییان ’کشف‘ را به معنی این میدانستند که چیزی را برای جلب توجه
اروپاییان دیگر مطرح کنند. یک پیشگامِ ریاضی صرفاً یک جنگلِ از قبل موجود را کاوش
نمیکند. حسی هست که میگوید آنها همانطور که جلو میروند جنگل خودشان را هم ایجاد
میکنند؛ گویی همانطور که قدم برمیدارند، گیاهان زیر پاهایشان جوانه میزنند، به
نهال، و سپس حتی ممکن است به درخت تنومندی تبدیل شوند.
من فکر میکنم که این هنوز هم منبع دیدگاه افلاطونی ایدههای ریاضی است: حقایق
ریاضی ’واقعاً‘ وجود دارند، ولی آنها به شکل ایدهآلی در یک نوع واقعیت موازی قرار
دارند، که همیشه وجود داشته و همیشه هم وجود خواهد داشت. بنابراین هنگامی که ما
قضیه جدیدی را اثبات میکنیم، ما تنها متوجه چیزی میشویه که برای مدتها پنهان
بوده. من تصور نمیکنم افلاطونگرایی معنی ملموسی داشته باشد، ولی بطور دقیقی روند
تحقیقات ریاضی را شرح میدهد. شما انتخابی ندارید: تنها کاری که میتوانید انجام
دهید این است که بوتهها را تکان دهید و ببینید چیزی از آنها بیرون میافتاد یا
نه. در کتاب واقعاً ریاضیات چیست؟ ریوبن هرش (Reuben Hersh) یک دیدگاه
واقعیتر را مطرح میکند و میگوید ریاضیات یک ساختِ ذهنی مشترکِ انسانی است. بر
این اساس، ریاضیات شبیه پول است. پول واقعاً در چند فلزات گرانبها، یا اسکناس، یا
اعدادی که در کامپیوتر ذخیره شده، خلاصه نمیشود؛ پول مجموعه مشترکی از
قراردادهایی است که شرح میدهد ما چگونه برای هر کالا یا پول دیگری، فلزات، اسکناسها،
و اعداد موجود در کامپیوترها را با هم مبادله میکنیم.
![]()
کتاب چهرههای برجسته یک کتاب تاریخی منظم از کلِ ریاضیات نیست، ولی
تلاش من بر این بوده تا موضوعات ریاضی را به شکل منسجمی مطرح کنم، بصورتی که هر چه
جلوتر میرویم مفاهیم بصورت نظاممندی پدیدار شوند. بطور کلی، چنین چیزی مستلزم
این است که موضوعات بترتیب تاریخی ارائه شوند. شرح موضوعات بصورت کاملاً موضوعی،
چیز غیرقابل درکی میشود، زیرا برای اینکار مجبوریم بطور دایم از یک ریاضیدان به
ریاضیدان دیگر برویم، بنابراین من فصول کتاب را به ترتیب تاریخِ تولدِ اشخاص مرتب
کردهام و اگر لازم بوده، به ریاضیدانان دیگر نیز اشاره دادهام.
چهرههای برجسته من، چه قدیمی چه جدید، چه مرد چه زن، چه غربی و چه شرقی، کلاً
شامل 25 نفر میشوند. زندگی این اشخاص در یونان باستان با هندسهدان و مهندس
یونانی ارشمیدس شروع میشود، کسی که دستآوردهای
او شامل طیف گستردهای از موارد میشود؛ از تخمین عدد π گرفته تا مساحت و حجم کره، تا پیچ ارشمیدس برای بالابردن آب و جنگافزارهای
منجنیقی برای نابود کردن کشتیهای دشمن. بعد از آن به سه نماینده از خاور دور میرسیم،
جایی که فعالیتهای اصلی ریاضی در قرون میانه در آنجا در جریان بود. این اشخاص
عبارتند از ادیب چینی لیو هوی، ریاضیدان ایرانی ابوموسی خوارزمی، که لغات ’الگوریتم‘ و ’جبر‘
از کارهای او برگرفته شده، و ریاضیدان هندی مادهاوا سانگاماگراما، که حدود 200 سال پیش از اینکه
کسانی مانند نیوتون در غرب از سریهای نامتناهی برای توابع مثلثاتی استفاده کنند،
او در این زمینه پیشگام بود.
فعالیتهای عمده ریاضی در طول دوران رونسانس به اروپا بازگشت، جایی که ما با
یکی از دغلبازترین چهرههای تاریخ ریاضیات، یعنی جرولامو کاردانو، برخورد خواهیم کرد. کاردانو، که شخصی قمارباز و جنجالی
بود، یکی از مهمترین کتابهای جبر که تا آن زمان منتشر شده بود را نیز نوشت، و کمی
هم طبابت کرد. او طالعبینی هم میکرد. برخلاف کاردانو، پییر دو فرما، که برای آخرین قضیه خودش معروف است، یک قاضی بود که
اشتیاق فراوانی به ریاضیات داشت، و این غالباً باعث میشد تا از کارهای حقوقی خودش
غافل بماند. فرما نظریه اعداد را به یکی از شاخههای رسمی ریاضیات تبدیل کرد. او
همچنین در نورشناسی کار کرد و یکی از اولین پیشگامانی بود که در توسعه حسابان نقش
داشتند. حسابان توسط نیوتون بارور شد. شاهکار نیوتون
کتاب اصول ریاضی فلسفه طبیعی است، که معمولاً به اصول (Principia)
کوتاه میشود. او قوانین حرکت و گرانش خودش را در این کتاب شرح داد، و از آنها
برای حرکت اجرام منظومه شمسی استفاده کرد.
یک قرن بعد از نیوتون، کانون ریاضیات به اروپای مرکزی و روسیه انتقال پیدا
کرد. در آن هنگام لئونارد اویلر، که بعنوان پربارترین
ریاضیدان تاریخ شناخته میشود، مقالات مهمی را منتشر کرد، و در بسیاری از حوزههای
ریاضیات کتابهای درسی نوشت که بسیار روشن و عالی بودند. هیچ حوزهای از ریاضیات
نبود که از چشم او دور بماند. اویلر حتی در ایدهایی سهیم بود که بعدها از طرف ژوزف فوریه مطرح شدند، و به انتقال حرارت
مربوط میشوند. بعدها این حوزه از ریاضیات به آنالیز فوریه معروف شد و یکی
از مهمترین شاخههای ریاضیات کاربردی را تشکیل میدهد. فوریه همچنین جزء اولین
کسانی بود که به نقش اتمسفر در تعادل گرمایی زمین پی برد.
با کارهای بینظیر کارل فردریش گاوس، که یکی از نامزدهای
عنوان بزرگترین ریاضیدان تاریخ است، ریاضیات پا به دوران جدیدش گذاشت. گاوس
کارهایش را با نظریه اعداد آغاز کرد، سپس جایگاهش در مکانیک سماوی را با پیشبینی
مکان سیارک سرس که به تازگی کشف شده بود مستحکم کرد، و پیشرفتهای عمدهای
را در حوزههایی مثل اعداد مختلط، روش کمترین مربعات، و هندسه نااقلیدسی حاصل کرد،
گرچه بدلیل نگرانیهایی که داشت و از این هراس داشت که جامعه ریاضی هنوز برای
پذیرش هندسههای نااقلیدسی آماده نیستند و ممکن است به مسخره گرفته شود، در
این مورد هیچ مطلبی منتشر نکرد. اعتماد به نفس نیکولای لوباچوفسکی بیشتر بود، و بطور گستردهای مقالاتی را درمورد
گونهای از هندسههای نااقلیدسی، که حالا هندسه هذلولی نامیده میشوند،
منتشر کرد. حالا او و یانوش بویویی بعنوان بنیانگذارانِ بحقِ
هندسه-نااقلیدسی، یعنی هندسه طبیعی یک سطح با انحناء ثابت، شناخته میشوند. اصولاً
گاوس درست تصور میکرد که این ایدهها جلوتر از زمان خودشان هستند، ولی او هیچگاه
نه از لباچفسکی نه از بویویی در طول حیات خودش تقدیر نکرد. در این دوره ما با
داستان غمانگیز ریاضیدان شورشی اواریست گالوا روبرو میشویم، که در سن
بیست سالگی طی یک نبرد تن به تن بر سر یک زن کشته میشود. او پیشرفتهای مهمی در
جبر حاصل کرد، که نهایتاً امروز به مفهوم حیاتی تقارن و گروههای تبدیل
منجر شد.
حالا با ورود اولین زن ریاضیدان، مضمون جدیدی به داستان ما وارد میشود، که
عبارت است از ریاضیات محاسباتی. اگوستا آدا کینگ، کُنتِس لاولیس، بعنوان دستیار چارلز
بابیج کار میکرد. او شخص مصممی بود که به قدرت بالقوه ماشینهای محاسبه پی
برده بود. چیزی که او در نظر داشت بسازد موتور تحلیلی نامیده میشود، یعنی
یک کامپیوتر قابلبرنامهریزی که از ضامنها و چرخدندهها ساخته شده بود. امروزه
آدا بطور گسترده بعنوان اولین برنامهنویس کامپیوتر شناخته میشود، هر چند این
ادعا کمی مناقشهانگیز است. مضمون کامپیوتر با جورج بول ادامه مییابد. بول با نوشتن کتاب قوانین فکر
پایههای صوری منطقِ دیجیتال، که اساسِ کامپیوترهای امروزی هستند را بنیان گذاشت.
همانطور که تنوع ریاضیات بیشتر میشود، داستان ما هم به حوزههای جدیدی از این
جنگلِ همیشه-رویان وارد میشود. برنهارت ریمان ریاضیدان بااستعدادی بود
که ایدههای سادهای که در پشت مفاهیم به ظاهر پیچیده قرار داشت را آشکار میکرد.
سهمی که او در ریاضیات داشت عبارت است از پایههای هندسه، خصوصاً
’مانیفولدها‘، که بعدها انیشتین در ارائه نظریه گرانش انقلابی خودش، موسوم به نسبیت
عام، از آن استفاده کرد. از کارهای مهم دیگر او میتوان به بکارگیری آنالیز
مختلط در نظریه اعداد اول اشاره کرد، که در آن نظریه اعداد و آنالیز مختلط از طریق
تابعی بنام زتا به هم ربط پیدا میکنند. فرضیه ریمان، که در مورد ریشههای
این تابع است، یکی از بزرگترین و مهمترین مسائل حلنشده در کل ریاضیات است، و یک
جایزه یک میلیون دلاری در انتظار کسی است که آن را حل کند.
سپس ما به گئورگ کانتور میرسیم. او با معرفی
نظریه مجموعهها باعث شد طریقه فکر کردن ریاضیدانان درباره اساسِ موضوعات ریاضی
تغییر کند، و با تعریف شمارش برای مجموعههای نامتناهی، به روشی کاملاً دقیق،
بامعنی، و مفیدی اثبات کرد که برخی از بینهایتها از بقیه بزرگتر هستند. کانتور
نیز ابتدا مانند بسیاری از مبتکران، جدی گرفته نشد و در طول زندگی خودش مورد تمسخر
قرار گرفت.
بعداً ما به دومین زن نابغه خودمان یعنی سوفیا کووالوسکایا بر میخوریم. زندگی او پیچیده بود و با سیاستهای انقلابی
روسیه، و موانعی که جامعه مرد-سالار در مقابل زنان قرار داده بود، در هم آمیخته
بود. واقعاً شگفتانگیز است که او اصلاً توانسته بود در ریاضیات دستآوردهایی
داشته باشد. در واقع، او کشفیات مهمی درباره حل معادلات دیفرانسیل جزئی، حرکت جسمِ
صُلب، ساختار حلقههای ذحل، و شکست نور توسط بلورها، انجام داد.
همگام با ورود به قرن بیستم، داستان ما نیز به ریاضیدان برزگ فرانسوی هانری پوانکاره میرسد. پوانکاره که مرد ظاهراً
عجیبی بود، حقیقتاً بسیار ژرف اندیش بود. او به اهمیت حوزه نوظهور توپولوژی (که به هندسه لاستیکی معروف بود و در آن اشکال میتوانند بطور پیوسته از ریخت
انداخته شوند) پی برد. او این شاخه را از دو بُعد به سه بُعد و بالاتر گسترش داد.
از آن برای حل معادلات دیفرانسیل استفاده کرد، و مسئله سه-جسم در گرانش نیوتونی را
مورد مطالعه قرار داد. مورد اخیر، او را به کشف امکان آشفتگیهای قطعی هدایت کرد،
که حاکی از این است که در یک سیستم غیر-تصادفی ظاهراً رفتار تصادفی دیده میشود.
او همچنین نزدیک بود تا نسبیت خاص را پیش از انیشتین کشف کند.
همتای پوانکاره در آلمان داوید هیلبرت بود، که دوران حرفهای او
را میتوان به پنج دوره مختلف تقسیم کرد. ابتدا او خط فکری بول را دنبال کرد، و بر
روی ’ تغییر ناپذیرها‘ کار کرد. تغییر ناپذیرها عبارات جبری هستند که در تغییر
مختصات نیز یکسان باقی میمانند. سپس او بصورت نظاممند به بهبود هسته نظریه اعداد
پرداخت. پس از آن، او اصول موضوعه اقلیدس را مورد بازنگری قرار داد، و چون آنها را
ناقص میدید، اصول موضوعه جدیدی را اضافه کرد تا خلاء موجود را پر کنند. سپس به
منطق و پایههای ریاضیات پرداخت و برنامهای را ترتیب داد که اثبات کند ریاضیات میتواند
بر اساس یک سری از اصول موضوعه پایهگذاری شود، و اینکه ریاضیات هم نامتناقض است
(هیچ استنتاج منطقی نمیتواند به یک تناقض منجر شود)، و هم کامل است (یعنی درستی
کلیه گزارهها میتواند اثبات یا رد شود). نهایتاً او به فیزیک ریاضی پرداخت، و
نزدیک بود در معرفی نسبیت عام گوی سبقت را از اینشتین برباید. او همچنین مفهوم
فضای هیلبرت را معرفی کرد، که در مکانیک کوانتوم بسیار مهم است.
امی نوتر سومین زن ریاضیدان ما
است، که در زمانی میزیست که هنوز مشارکت زنان در امور دانشگاهی از طرف مردان شاغل
در این حوزهها طرفداران زیادی نداشت. او نیز مانند هیلبرت کارش را با نظریه
تغییرناپذیرها آغاز کرد، و بعداً همکار او شد. هیلبرت تلاش فراوانی کرد که این سقف
شیشهای را بشکند و در دانشگاه برای نوتر یک سِمت دائمی را فراهم آورد. نوتر زبانههای
جبر مجرد را برافروخت، و پیشرو استفاده از ساختارهایی همچون گروهها، حلقهها، و
میدانها شد. او همچنین قضیه بسیار مهمی را اثبات کرد که تقارن قوانین فیزیک را با
کمیتهای پایا، مثل انرژی، مرتبط میساخت.
در اینجا داستان به قرن بیستم میرسد. ما برای اینکه اثبات کنیم تواناییهای
ریاضی فقط به طبقه تحصیلکرده غربی منحصر نمیشود، زندگی یک نابغه خودآموخته بنام سرینیواسا رامانوجان را دنبال میکنیم، که
زندگی خود را در فقر گذاراند. توانایی او در درک فرمولهای درست بینظیر بود و
شاید بتوان آن را فقط با کسانی مثل اویلر و کارل ژاکوبی مقایسه کرد. برای
رامانوجان مفهوم اثبات خیلی دقیق نبود، ولی میتوانست فرمولهایی را پیدا کند که
هیچ کسی حتی خواب آنها را نمیدید. مقالات و دفترهای او هنوز هم مورد مطالعه
هستند.
بعداً به دو ریاضیدان میرسیم که تمایلات فلسفی دارند و ما را به پایههای
ریاضیات و ارتباط آن با حساب میرسانند. یکی از آنها کورت گودل است، که اثبات کرد هر سیستمِ اصلموضوعی برای حساب ناکامل
و تصمیمناپذیر است. او با اینکار رویای هیلبرت، که میخواست خلاف این را اثبات
کند، را ویران ساخت. ریاضیدان دیگر آلن تورینگ است، که تحقیقاتش درباره
کامپیوترهای قابلبرنامهریزی بسیار مهم است. البته او بیشتر برای فعالیتهایی که
در طول جنگ جهانی دوم برای شکستن رمز آلمانها انجام داد معروف است. او همچنین
برای سنجش هوش مصنوعی آزمونی را پیشنهاد داد که اکنون به آزمون تورینگ
معروف است. او بعد از جنگ نیز بر روی الگوهایی کار کرد که در مورد تعیین هویت
حیوانات کاربرد داشت. تورینگ همجنسگرا بود و نهایتاً در شرایط غمانگیز و
اسرارآمیزی جان سپرد.
تصمیم من بر این بود که هیچ یک از ریاضیدانان زنده را در این کتاب نگنجانم،
ولی نهایتاً کتاب را با دو تن از ریاضیدانانی که به تازگی فوت شدهاند به پایان
رساندم. یکی از آنها در حوزه ریاضیات محض، و دیگری در حوزه ریاضیات کاربردی فعالیت
میکردند. اولی بنوآ مندلبرو است، که عموماً برای
کارهایش درمورد فراکتالها معروف است. فراکتالها اشکال هندسی هستند که در صورت
بزرگنمایی نیز ساختارهای پیچیدهای دارند. غالباً فراکتالها نسبت به سطوح
ساده، مثل کره یا استوانه، مدل خیلی بهتری برای طبیعت هستند. هرچند ریاضیدانان
دیگری نیز بر روی ساختارهایی که ما حالا آنها را فراکتال میشناسیم کار کرده
بودند، ولی این مندلبرو بود که به قدرت بالقوه آنها در مدلسازی جهان طبیعی پی برد.
او جزء ریاضیدانانی نبود که خیلی عاشق اثبات ریاضی باشند؛ در عوض او از هندسه نوعی
درک بصری داشت، که او را به این هدایت کرد که ارتباطات را ببیند و حدسهای را مطرح
کند. او همچنین کمی اهل نمایش بود، و با اشتیاق ایدههای خودش را تبلیغ میکرد.
اینها باعث نمیشد که او در میان برخی ریاضیدانان محبوب باشد، ولی مسئله این است
که شما نمیتوانید همه را خشنود کنید.
نهایتاً من ویلیام تورستون را انتخاب کردهام که در
حوزه ریاضیات محض کار میکرد. تورستون نیز درک شهودی عمیقی از هندسه داشت، به نوعی
عمیقتر از مندلبرو. او میتوانست بر روی ریاضیاتی کار کند که بخوبی قضایا در آن
اثبات شده بودند، گرچه در این اواخر او بیشتر بر روی قضایا تمرکز میکرد و طرح
اثبات آنها را میریخت. او به ویژه بر روی توپولوژی کار کرد، و به ارتباط غیر
منتظره آن با هندسه-نااقلیدسی پی برد. نهایتاً مجموع این ایدهها گریگوری
پرلام را برانگیخت تا حدسی را که پوانکاره مطرح کرده بود را اثبات کند. روشهای
او همچنین یکی از حدسهای تورستون را اثبات کرد که رهیافتهای مهمی را در رابطه
با کلیه مانیفولدهای سه-بعدی فراهم میآورد.
![]()
در فصل آخر من برخی از ایدههایی را
مطرح کردهام که به داستانهای این 25 شخص برجسته ربط دارند، و خواهم گفت که آنها
درباره ریاضیدانان پیشگام به ما چه خواهند گفت – آنها
که هستند، چگونه کار میکنند، ایدهای دیوانهوار خودشان را از کجا میگیرند، و
محرک آنها برای اینکه اصلاً یک ریاضیدان باشند چیست.
ولی فعلاً مایلم در اینجا دو هشدار را مطرح کنم. اول اینکه کار من ضرورتاً
حالت گزینشی داشته. مطرح کردن زندگینامه جامع ریاضیدانان، بررسی کامل کلیه مواردی
که آنها برروی آن کار کردهاند، یا وارد شدن به جزئیات دقیق اینکه چگونه ایدههای
آنها تکامل یافته، و یا چگونه با همکاران خودشان تعامل میکردند، همه مواردی هستند
که هیچ موقع امکان مطرح کردن آنها در کتابی با این حجم نخواهد بود. در عوض سعی من
بر آن بوده که گزیدهای از مهمترین، یا جالبترین کشفیات آنها را با جزئیات تاریخی
کافی عرضه کنم تا تصویری از آنها و جامعهای که در آن زندگی میکردند را ترسیم
کنم. حتی برای برخی از ریاضیدانان عهد باستان، بدلیل در دست نبودن مدارک کافی
درباره زندگی آنها، مطالب ارائه شده بسیار سطحی و خالی از جزئیات هستند.
دوم اینکه 25 نفر ریاضیدانی که من انتخاب کردهام، به هیچ وجه تنها اشخاص
برجستهای نیستند که در توسعه ریاضیات نقش داشتهاند. من برای گزینش این اشخاص
دلایل زیادی داشتهام، از جمله اهمیت کشفیات آنها، جالب بودن حوزه مربوطه، گیرایی
داستان زندگی آنها، دوره تاریخی که در آن میزیستهاند، تنوع کارها، و ’توازن‘
میان آنها. اگر ریاضیدان مورد علاقه شما در میان اینها نیست، احتملاً مهمترین دلیل
آن کمبود جا، و همچنین تلاش برای انتخاب نمایندگانی بوده که بطور گسترده در یک
مانیفولد سه-بعدی توزیع شدهاند که مختصات آن عبارت است از، جغرافیا، دوره تاریخی،
و جنسیت. من براین باورم که تمام کسانی که از آنها نام برده شده شایسته این بودهاند
که در این کتاب شامل شوند، هر چند بر سر انتخاب یکی دو نفر از آنها ممکن اختلاف
نظر وجود داشته باشد. هیچ تردیدی ندارم که با همین توجیه کسان دیگری هم میتوانستند
انتخاب شوند.
بهار 2018، یان استوارت

ارشمیدس (Archimedes of Syracuse): تولد: حوالی 287 پیش از میلاد سیراکیوز، سیسیل. وفات: حوالی 212 پیش از میلاد،
سیراکیوز.
زمان
سال 1973 بود و مکان پایگاه دریایی
سکاراماگاس، در نزدیکی آتن. همه نگاهها بر روی ماکت یک کشتی چوبی متمرکز شده. در
آنجا هفتاد آینه مس-اندود بودند که در فاصله پانزده متری یکدیگر قرار داشتند، و هر
کدام یک متر عرض و نیم متر ارتفاع دارند. پرتوهای نور خورشید از روی این آینهها
منعکس شده و در مکانی متمرکز میشود که کشتی چوبی در آنجا قرار داشت.
در عرض چند ثانیه کشتی شعلهور میشود.
یک دانشمند یونانی معاصر بنام یوآنیس ساکاس (Ioannis Sakkas)
مشغول آفرینش حماسهای است که در علوم یونان باستان آمده است. یک نویسنده رومی
بنام لوثین (Lucian) مینویسد در زمان محاصره سیراکیوز در حوالی سالهای 214-212 پیش
از میلاد، ریاضیدان و مهندس یونانی ارشمیدس دستگاهی را اختراع کرد که با آتش زدن
کشتیهای دشمن آنها را نابود میکرد. بر سر اینکه آیا واقعاً چنین دستگاهی وجود
داشته، و اگر هم وجود داشته چگونه کار میکرده، هنوز هم بحث هست. داستان لوثین میتواند
تنها به استفاده از پیکانها یا گویهای آتشینی اشاره کند که از یک منجنیق پرتاب
میشدند، ولی مشکل میتوان دید که چرا از این بعنوان یک اختراع جدید نام برده میشود.
در قرن ششم بعد از میلاد آنتمیوس (Anthemius) در کتاب شیشههای
سوزان این پیشنهاد را مطرح میکند که ارشمیدس از یک عدسی بسیار بزرگ استفاده
کرده. ولی به احتمال قویتر، او از یک آینه بزرگ، یا شاید از آرایهای از آینههای
کوچک استفاده کرده که بصورت یک کمان چیده شدهاند تا یک سهمی انعکاسی را شکل دهند.
سهمی (parabola) یک منحنی U-شکل است که برای هندسهدانان یونانی
بخوبی شناخته شده بود. ارشمیدس نیز مطمئناً از خواص کانونی آن اطلاع داشت. کلیه
خطوطی که با محور یک سهمی موازی باشند، هنگام انعکاس در آن، از یک نقطه بنام کانون
عبور میکنند. اینکه کسی متوجه شده باشد یک آینه سهمیشکل میتواند نور، یا
گرمایی، که از خورشید میرسد را به همین شکل کانونی کند زیاد معلوم نیست، زیرا درک
یوناییان از نور ابتدایی بود. ولی همانطور که آزمایش ساکاس نشان داد، در واقع
ارشمیدس به یک چیدمان سهمیشکل نیاز نداشت. اگر تعداد زیادی از سربازان که هر کدام
یک سپر منعکس کننده در دست دارند بطور مستقل آن را به سمت خورشید هدف بگیرند، طوری
که تا نور آنها در یک نقطه از کشتی متمرکز شود، این نیز بطور موثری جواب میدهد.
عملی بودن چیزی که به ’پرتو گرمایی ارشمیدس‘ معروف است، خیلی مورد بحث بوده.
فیلسوف معروف، رنه دکارت، که یکی از پیشگامان حوزه نورشناسی بود، اعتقاد داشت که
چنین چیزی عملی نیست. آزمایش ساکاس نشان داد که چنین چیزی ممکن است، ولی کشتی
قلابی او نازک بود، و بدلیل اینکه با رنگِ روغنی پوشیده بود، به آسانی شعلهور میشد.
ولی در زمان ارشمیدس نیز معمول بود که برای محافظت از بدنه کشتی آن را قیر اندود
کنند. در سال 2005، جمعی از دانشجویان دانشگاه ام.آی.تی آزمایش ساکاس را تکرار
کردند، و نهایتاً یک کشتی چوبی قلابی را به آتش کشیدند – ولی
اینکار فقط وقتی انجام شد که کشتی در سکون کامل بود و به مدت ده دقیقه در زیر
کانون قرار داشت. آنها بار دیگر در سانفرانسیسکو با استفاده از یک قایق
ماهیگیری برای برنامه تلویزیونی Mythbusters این آزمایش را تکرار کردند، و موفق شدند چوب آن را
ذغال کنند و چند شعله هم از آن برخواست، ولی بطور کامل شعلهور نشد. دستاندر
کاران برنامه تلویزیونی Mythbusters به این نتیجه رسیدند که
این حکایت افسانهای بیش نبوده.
![]()
ارشمیدس یک علامه بود: منجم، ریاضیدان، مهندس، مخترع، فیزیکدان. او احتمالاً
بزرگترین دانشمند عصر خودش بود. علاوه بر کشفیات مهم ریاضی که داشت، او اختراعات
مهیجی را نیز انجام داد، چیزهایی مثل: پیچ ارشمیدس برای بالا بردن آب، طناب و
قرقره برای بلند کردن اجسام سنگین. او قانون اهرمها، و همچنین چیزی را کشف کرد که
امروزه اصل ارشمیدس نامیده میشود و درمورد جابجایی مایعات است. ساختن یک
دستگاه جرثقیل-مانند که از آن در نبرد سیراکیوز استفاده شده و میتوانست کشتیهای
دشمن را از آب بلند کرده و آنها غرق کند، نیز به او نسبت داده میشود. در
سال 2005 در برنامه مستند ابر سلاحهای جهان باستان نمونهای از این دستگاه
ساخته شد که جواب میداد. در متون باستانی به بسیاری دیگر از قضایا و اختراعاتی
اشاره میشود که آنها را به ارشمیدس نسبت میدهند. در میان آنها یک ماشین محاسبه
نجومی است، که شباهت زیادی به آنتیکیترا (Antikythera) دارد که در
سال 1900 در بقایای یک کشتی غرق شده پیدا شد، و مکانیزم آن تا همین اواخر نامعلوم
بود.
ما درباره زندگی ارشمیدس اطلاع زیادی نداریم. او در یکی از شهرهای تاریخی
سیسیل بنام سیراکیوز (Syracuse) بدنیا آمد. این شهر در سال 734 یا 733 پیش از میلاد هنگامی که
آرکیاس از کورینس تبیعد شد، توسط مهاجرین یونانی تاسیس شد. بر طبق گفته تاریخنگار
یونانی، پلوتارک (Plutarch)، آرکیاس شیفته پسر زیبایی بنام آکتیون شد. هنگامی که درخواستهای
او از طرف پسر جوان رد شد، او سعی کرد که او را برباید، و طی یک منازعه، اکتیون
تکه پاره شد. هیچوقت به درخواستهای پدرش ملیسوس برای اجراء عدالت پاسخ داده نشد،
بنابراین او به بالای معبد پوسایدون (Poseidon) رفت و از
خدایان خواست تا انتقام خون پسرش را بگیرند. او خودش را از آن بالا به سنگهای
پایین معبد انداخت. بدنبال این وقایع اندوبار، قحطی و خشکسالی شدیدی آنجا را فرا
گرفت، و پیشگویان محلی اعلام کردند که این فقط انتقام است که میتواند خشم پوسایدون
را فرو نشاند. آرکیاس این پیام را گرفت، و بطور داوطلبانه خودش را به سیسیل تبعید
کرد، و در آنجا سیراکیوز را بنا کرد. بعدها گذشته او گریبانش را گرفت، و توسط پسری
بنام تلفوس، که او نیز توجه آرکیاس را بخودش جلب شده بود، کشته شد.
سیراکیوز سرزمین حاصلخیزی بود، و بزودی به یکی از آبادترین و قدرتمندترین
شهرهای یونان در کل مدیترانه تبدیل شد. ارشمیدس در کتاب شِن شمار میگوید
که پدرش فیدیاس یک منجم بوده. بر طبق گفته پلوتارک، او یکی از اقوام دور هایرو دوم،
حاکم ستمگر سیراکیوز بود. حدس زده میشود که ارشمیدس در جوانی در دانشگاه
اسکندریه، که در سواحل دلتای نیل قرار داشت، تحصیل کرده باشد. در آنجا او با کسانی
همچون کونون ساموسی (Conon
of Samos) و اِراتوستِن (Eratosthenes)
آشنا شد. مدرکی که برای این مورد در دست است، نقل قولی از ارشمیدس است که میگوید
کونون یک دوست بود؛ او همچنین در کتاب روش قضایای مکانیکی و مسئله
احشام به اِراتوستِن اشاره میکند.
درباره مرگ ارشمیدس نیز داستانهای وجود دارند، که من بعداً به آنها اشاره
خواهم کرد.
![]()
اعتبار ریاضی ارشمیدس بر آثاری تکیه دارند که از او باقی ماندهاند، و همه
آنها بصورت کپیهایی هستند که بعداً نگاشته شدهاند. کتاب تربیع سهمی، که
به شکل نامهای است که او به دوست خودش دوسیتِوس نوشته، حاوی 24 قضیه
درباره سهمی هستند، که در قضیه آخر، مساحت بخشی از یک سهمی را بصورت مساحت یک مثلث
بیان میکند. سهمی نقش عمدهای در کارهای او دارد. سهمی گونهای از مقاطع مخروطی (conic section)
است. اینها منحنیهایی هستند که نقش عمدهای در هندسه یونانی بازی میکردند. برای
ایجاد یک مقطعِ مخروطی، شما باید از صفحهای استفاده کنید که یک مخروط مضاعف
را قطع کند. سه نوع مقطعِ مخروطی اصلی وجود دارد: بیضی (ellipse)، سهمی (parabola)، و هذلولی (hyperbola). بیضی بصورت یک
دایره فشرده است. سهمی بشکل U است، و هذلولی نیز بصورد دو منحنی U شکل هستند که پشت
هم قرار دارند.
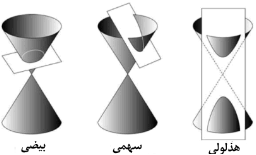
سه گونه از مقاطع مخلروطی
اصلی
کتاب تعادل
صفحه حاوی دو جلد جداگانه است. در این کتاب برخی از نتایج اساسی در مورد فیزیک
مطرح میشوند که ما حالا به آن علم سکون شناسی یا استاتیک (statics)
میگوییم. استاتیک شاخهای از مکانیک است که به تحلیل شرایطی میپردازد که یک جسم
در حالت سکون باقی میماند. توسعه آتی این موضوع پایههای کلی مهندسی راه و
ساختمان را بنا نهاد، و امکان این را فراهم آورد که نیروهای وارده بر روی
اجزاء ساختاری ساختمانها و پلها محاسبه شوند، تا اطمینان حاصل شود که بجای اینکه
آنها تاب بردارند یا فروبریزند، واقعاً در حال سکون باقی میمانند.
اولین جلد
کتاب بر روی قوانین اهرمها تمرکز میکند، و در آن ارشمیدس میگوید: ”اجسام در
فاصلهای درحال تعادل قرار میگیرند که با وزن آنها نسبت معکوس دارد.“ اولین پیامد
این حرف این است که یک اهرم بزرگ میتواند نیروی کوچکی را تقویت کند. پلوتارک میگوید
که ارشمیدس در نامهای که به هریون نوشت این موضوع را بصورت غلو آمیز چنین بیان میکند:
”به من جایی برای ایستادن دهید، من زمین را جابهجا خواهم کرد.“ برای اینکار او به
اهرم بسیار بلندی نیاز دارد، که کاملاً محکم باشد. ولی اشکال اینکار این است که
گرچه اهرم نیروی وارده را تقویت میکند، ولی نسبت به سمتی که نیرو به آن وارد میشود،
سمت دیگر اهرم حرکت بسیار کندتری را خواهد داشت. اگر بنا باشد زمین تا این اندازه
(بسیار-بسیار کم) جابجا شود، ارشمیدس میتوانست فقط با بالا/پایین پریدن هم اینکار را انجام دهد.
با این همه، اهرم دستگاه کارآمدی است. قرقره نوع دیگری از اهرمها است، که ارشمیدس
به آن پی برده بود، به اندازه اهرم کارآمد است. هنگامی که هریونِ شکاک از ارشمیدس
خواست تا این را برایش نمایش دهد، ارشمیدس برای اینکار کشتی بزرگی را انتخاب کرد،
آن را پر از مسافر و کالا نمود، سپس خودش دورتر در لنگرگاه ایستاد و درحالی که سر
قرقره را در دست داشت، کمی طنابها را کشید، و با اینکار به آرامی کشتی را در یک خط
مستقیم بالا کشید، انگار در دریا حرکت میکرد.
کتاب دوم عمدتاً درباره یافتن مرکز ثقل اشکال مختلفی مثل مثلث، متوازيالاضلاع،
ذوذنقه، و بخشهایی از یک سهمی است.
کتاب در باب کره و استوانه حاوی نتایجی است که ارشمیدس چنان به آنها
مفتخر بود که وصیت کرد آنها را بر مقبرهاش حک کنند. او با دقت زیادی اثبات کرد که
مساحت یک کره چهار برابر هر یک از دایرههای عظیمه آن (مثل دایره استوایی کره
زمین) است؛ و حجم آن دو سوم استوانهای است که کره را بطور تنگاتگ در بر میگیرد؛
و اینکه مساحت هر قطاع کروی که از قطع شدن یک صفحه با یک کره حاصل میشود برابر بخشی
از چنین استوانهای است. اثبات او بر پایه روش پیچیدهای قرار داشت که افنا (exhaustion)
نامیده میشود، و برای کار با نسبتهایی که شامل اعداد غیرگویا هستند توسط ادوکسوس
ابداع شد. به زبان امروزی، او ثابت کرد که مساحت یک کره که شعاع آن r است، برابر 4πr2، و
حجم آن برابر 4⁄3πr3 است.
ریاضیدانان عادت دارند که نتایج نهایی خودشان را بصورتی کاملاً شسته رفته و
بشکلی زیبا و سازمان یافته ارائه دهند، و غالباً از نشان دادن روندهای آشفتهای که
آنها را به این تنایج رسانده اجتناب میکنند. ولی ما بخت این را داریم که با جزئیات
روندهایی آشنا شویم که ارشمیدس را به چنان نتایجی رهنمون کرده. اینها در کتابی
بنام روش قضایای مکانیکی ثبت شدهاند. برای مدتها تصور میشد که این اثر گم
شده است، ولی در سال 1906 تاریخنگار دانمارکی یوهان هایبرگ (Johan Heiberg)
نسخه ناقصی از آن را در یک چندنگاره (palimpsest) کشف کرد.
چندنگاره کاغذی بود که در دوران باستان بارها پاک یا شسته میشد تا نویسنده بتواند
با نوشتن متون جدید، از آن مجدداً استفاده کند. کارهای ارشمیدس در سال 530 بعد از
میلاد توسط ایزیودوروس در قسطنطنیه پایتخت امپراطوری بیزانس (استانبول فعلی)
گردآوری شدند. در حوالی سالهای 950، در زمانی که لئوی هندسهدان (Leo the Geometer) یک
مدرسه ریاضی تاسیس کرده بود تا در آن آثار ارشمیدس مورد مطالعه قرار گیرند، از روی
آنها کپی برداری شد. در سال 1229 این چندنگاره سر از اورشلیم درآورد، و در
آنجا شسته شد (البته نه بصورت کامل)، سپس از وسط تا خورد، و برای نوشتن یک کتابِ
دعای مسیحی 177-صفحهای مجددا مورد استفاده قرار گرفت.
در دهه 1840 این چندنگاره به دست یک ادیب مسیحی بنام کنستانتین فون تیشندورف
افتاد، و او متوجه نوشتههای کم رنگی بر روی آن شد که حاکی از ریاضیات یونانی
بودند. او یک صفحه از آن را برداشت و آن را به کتابخانه دانشگاه کمبریج فرستاد. در
سال 1899 بخشی از این صفحه ترجمه شد. هایبرگ با دیدن آن متوجه شد که کار ارشمیدس
است، و برای عکسبرداری از کل چندنگاره به استانبول باز گشت. سپس از روی آن رونوشت
برداشت، و نتایج آن را بین سالهای 1910 تا 1915 منتشر کرد. سپس توماس هیث
(Thomas Heath) این متن را به انگلیسی ترجمه کرد. پس از یک سری از دعواهای حقوقی
که بر سر مالکیت آن صورت گرفت، سرانجام در یک حراج، یک آمریکایی ناشناس این اثر را
به مبلغ 2 میلیون دلار خریداری کرد. مالک جدید به دانشمندان اجازه داد تا آن را
بطور دقیق مطالعه کنند، و از آن زمان تاکنون از تکنیکهای مختلف تصویربرداری
دیجیتال برای آشکارسازی متون زیرِ آن استفاده شده.
روش افنا نیاز به این دارد تا شما از قبل جواب صحیح را بدانید، و دانشمندان
مدتها متعجب بودند که چطور ارشمیدس توانسته مساحت و حجم کره را حدس بزند. او در
کتاب روش قضایای مکانیکی چگونگی اینکار توضیح داده میشود:
برخی از چیزها از طریق بکارگیری یک روش مکانیکی برای من آشکار میشوند، هرچند
نتایج آنها نهایتاً باید توسط هندسه اثبات شوند، زیرا تحقیق با این روشها اثبات
واقعی را فراهم نمیآورد. ولی البته هنگامی که ما با استفاده از این روشها نتایج
را بدست آوردیم، فراهم آوردن اثبات بسیار
آسانتر خواهد بود.
ارشمیدس میپنداشت که با قرار دادن یک کره، یک استوانه، و یک مخروط در یک
ترازو، و سپس تقسیم آنها به قطعات بسیار کوچک که تعادل ترازو را نگاه دارند. سپس
او از قوانین اهرمها برای ارتباط دادن این سه حجم استفاده کرد (قوانین مربوط به
استوانه و مخروط در آن زمان شناخته شده بودند) و از این طریق کمیتهای مورد نظر
خودش را بدست آورد. گفته میشود که ارشمیدس پیشگام استفاده از ’بینهایتهای
حقیقی‘ در ریاضیات بود. ممکن است از یک سند نامفهوم نتوان چنین چیزی را نتیجه
گرفت، ولی روشن است که در چندنگاره مذکور از برخی از ایدههای حسابان استفاده شده
است.
![]()
کارهای دیگر ارشمیدس نشان میدهد که علایق او تا متنوع بوده. در کتاب درباب
مارپیچها، او طول و مساحت چیزی که بنام مارپیچ ارشمیدس معروف است را
اثبات میکند. مارپیچ ارشمیدس یک منحنی است که توسط نقطهای توصیف میشود که با
سرعت یکنواخت در طول خطی حرکت میکند که خودش با سرعت یکنواخت در حال دوران است.
در کتاب مخروطها و شبهکرهها، او حجم بخشهایی از اجسام را بررسی میکند
که از دوران یک مقطع مخروطی حول یک محور حاصل میشوند.
کتاب درباب اجسام شناور، جزء اولین کارهایی است که درباره هیدرواستاتیک
(hydrostatics)، یا علم نقاط تعادل اشیاء شناور، صورت گرفته. این شامل اصل
ارشمیدس نیز هست که میگوید: نیروی رو به بالای وارد بر جسمی که در یک مایع (یا
گاز) فرو میرود، با وزن مقداری از مایع که بر اثر فرورفتن جسم جابهجا شده است
برابر است. موضوع ضربالمثل معروف ”یافتم، یافتم“ نیز همین اصل است. از ارشمیدس
خواسته میشود که مشخص کند آیا تاج ساخته شده برای شاه هِیرو دوم، حقیقتاً از طلا
است یا نه. او که در حمام نشسته بود، چنان از یافته خودش به هیجان آمد که بدون
لباس از حمام بیرون آمد و در خیابان فریاد زد ’ Eureka!, Eureka!‘، یعنی ’یافتم!، یافتم!‘. باید توجه داشته باشید که در آن زمان لخت ظاهر شدن
در مکانهای عمومی کار بسیار ناپسندی بود. از نظر فنی، نقط اوج این کتاب جایی است
که شرط تعادل یک سهمیگونِ (paraboloid) شناور را
توضیح میدهد. این از اولین کارهایی بود که درباره معماری کشتیها صورت میگرفت، و
برای ثبات و عدمواژگونی آنها اهمیت داشت.
کتاب اندازهگیری دایره از روش افنا استفاده میکند تا ثابت کند مساحت
دایره با نصف شعاع ضرب در محیط آن، یا به زبان امروزی πr2، برابر است. برای اثبات اینمورد، ارشمیدس چندضلعیهای منظم 6، 12، 24، 48، و 96
ضلعی را هم در دایره محاط، و هم بر آن محیط کرد. با در نظر گرفتن 96-ضلعی،
او ثابت کرد که نتیجهای که برای π حاصل میشود، بطور تقریبی میان 31/7 و 310/71 قرار میگیرد.
او کتاب شِن شمار را به حاکم ستمگر سیراکیوز، گلو دوم پسر هِیرو دوم،
تقدیم میکند. این مدرکی بر این است که ارشمیدس با دربار سلطنتی در ارتباط بوده:
شاه گلئو، برخی تصور میکنند که تعداد دانههای شن دنیا بینهایت
است... ولی من سعی خواهم کرد بوسیله اثبات هندسی به شما نشان دهم که اعدادی که
توسط من نامگذاری شدهاند، و آنها را برای زئوکسیپیوس (Zeuxippus) فرستادهام، برخی از آنها نه فقط
از تعداد شنهای روی زمین بلکه از جرمی معادل کل جهان هستی نیز بزرگتر هستند.
در اینجا ارشمیدس به دستگاه جدید خودش برای نامگذاری اعداد بزرگ اشاره میکند
و میخواهد سوء برداشت رایجی که میان ’بینهایت‘ و ’بسیار زیاد‘ وجود دارد را رفع
کند. او میان این دو تمایز آشکاری را برقرار میکند. او در کتابش این دو ایده اصلی
را در هم ادغام میکند. اولی توسعه اعداد استاندارد یونانی است که بتوان از آنها
برای نامگذاری اعداد بسیار بزرگ بهره گرفت (در آن زمان بزرگترین عدد 100 میلیون
بود که به آن میرییاد myriad میگفتند). دومی بدست دادن برآوردی برای اندازه جهان است، که او
آن را بر پایه نظریه خورشیدمرکزی (heliocentric) آریستارکس
(Aristarchus) مطرح کرد. اگر بخواهیم نتایجی که ارشمیدس حاصل کرد را بصورت
نمادگذاریهای جدید بیان کنیم، برای پر کردن جهان به حداکثر 1063
دانه شن نیاز است.
![]()
مدارکی موجود درباره زندگی ارشمیدس بسیار اندک هستند، ولی با فرض اینکه داستانها
درست باشند، ما درباره مرگ او اطلاع بیشتری داریم، که احتمالاً منعکس کننده حداقلی
از حقیقت هستند.
در دومین نبرد پونیک، که در حوالی سالهای 212 پیش از میلاد رخ داد، ژنرال
رومی مارکوس کلادیوس مارسلوس، محاصره سیراکیوز را آغاز کرد، و پس از دو سال
توانست آن را تسخیر کند. پلوتارک نقل میکند که ارشمیدسِ
پیر مشغول نگاه کردن به اشکال هندسی بود که بر روی شنها رسم کرده بود. ژنرال
سربازی را فرستاد تا از ارشمیدس بخواهد با او ملاقات کند، ولی ریاضیدان با ناراحتی
به او گفت که هنوز کارش بر روی مسئله تمام نشده. سرباز نیز عصبانی شد و با شمشیرش
ارشمیدس را کشت. آخرین کلماتی که حکیم به زبان آورد این بود ” سایهات را از دایرههای
من دور کن!“ با شناختی که از این ریاضیدان داریم، چنین چیزی کاملاً محتمل است، ولی
پلوتارک روایت دیگری را ارائه میدهد که گفته میشود ارشمیدس میخواسته خودش را به
سرباز تسلیم کند، ولی سرباز پیش خودش تصور میکرده که ابزارهای ریاضی که ارشمیدس
با خودش حمل میگرده با ارزشاند، و برای اینکه آنها را سرقت کند او را کشته. هر
کدام از دو روایت درست باشد، باز هم مارسلوس تاحدی از مرگ این مهندس نابغه ناراحت شد.
مقبره ارشمیدس با حکاکی یکی از قضایای موردعلاقه او که در کتاب درباب کرهها
و استوانهها آمده تزیین شده بود: کرهای که در یک استوانه محاط شده، حجمی
برابر دو سوم آن استوانه و مساحتی برابر با آن دارد. یک قرن پس از مرگ ارشمیدس،
خطیبِ معروفِ رومی سیسرو (Cicero) در سیسیل
سرپرست امور مالیاتی بود.در آن زمان این مقبره وضعیت خوبی نداشت و خراب شده بود.
او که چیزهایی در مورد مقبره شنیده بود، دستور داد تا بازسازی شود، و توانست برخی
از حکاکیهای آن، از جمله نمودار کره و استوانه، را بخواند.
امروزه محل دقیق این مقبره معلوم نیست، و بنظر نمیرسد هیچ چیزی از آن بجا
مانده باشد. ولی ارشمیدس بواسطه ریاضیاتی که به جهان ارئه داد زنده است، ریاضیاتی
که پس از گذشت بیش از دو هزار سال هنوز هم مهم است.

لیو هوی (Liu Hui): تولد: حوالی قرن سوم
میلادی کائو وی، چین.
کتاب 周髀算經 (یا حساب کلاسیک عقربهها و مسیرهای آسمان) قدیمیترین متن ریاضی
شناخته شده چینی است که قدمت آن به سالهای 400 تا 200 پیش از میلاد باز میگردد،
دورانی که چین در جنگ به سر میبرد. این کتاب با یک مقدمه تبلیغاتی آغاز میشود:
مدتها پیش، رونگ فنگ از شن ژی پرسید ’استاد، اخیراً مطالبی در
مورد طریقت شما شنیدهام. آیا این درست است که با استفاده از این طریقت قادر خواهیم
بود ارتفاع و اندازه خورشید، یا مساحتی که توسط پرتوهای آن روشنشده، یا میزان
حرکت روزانه آن، یا تخمینی برای نزدیکترین یا دورترین فاصله آن، حد بینایی انسان،
یا صور فلکی که ستارگان در آن بصورت مرتب قرار دارند، و طول و عرض زمین و آسمان را
اندازه بگیریم؟‘
شن ژی گفت ’حقیقت دارد،‘.
رونگ فنگ پرسید ’استاد، گرچه من باهوش نیستم، ولی مایلم مرا توجیه کنید. آیا
کسی مثل من میتواند این طریقت را فرا گیرد؟‘
شن ژی جواب داد ’آری، تو میتوانی از طریق ریاضیات به همه چیز دست پیدا کنی.
اگر تو خالصانه درباره آنها مرتباً فکر کنی، توانایی تو در ریاضیات برای درک چنین
موضوعاتی کفایت میکند‘.
کتاب از هندسه استفاده میکند و با طرح یک شکل برای نشان دادن فاصله زمین از
خورشید ادامه مییابد. مدل کیهانشناسی بکارگرفته شده در آن بسیار ابتدایی بود،
بصورتی که یک زمین مسطح در زیر صفحه یک آسمان گرد قرار داشت. ولی ریاضیات
بکارگرفته شده بسیار پیچیده بود. اساساً در این روش از مثلثهای متشابه استفاده میشد
تا سایههایی که توسط خورشید ایجاد میشد را نشان دهد.
کتاب فوق، که به ژو بی (Zhou
Bi) معروف است، وضعیت پیشرفت ریاضیات
چینی را در زمان یونان باستان، یعنی از زمان مرگ اسکندر در سال 323 ق.م تا زمانی
که جمهوری رم در سال 146 ق.م یونان را به خودش ضمیمه کرد، نشان میدهد. این دوران
اوج تسلطِ فرهنگی یونان باستان بود؛ یعنی دوران هندسهدانان، فیلسوفان، منطقدانان،
و منجمین بزرگ جهان باستان. یونان حتی تحت سلطه روم نیز در حوزههای علم و فرهنگ
تا سالهای 600 ب.م نیز به پیشرفت خود ادامه داد، ولی مرکز ابدعاتِ ریاضی به چین،
خاورمیانه، و هند منتقل شد. پیشرفتهای مهم ریاضی تا دوران رونسانس به اروپا باز
نگشتند، هر چند دورانی که در اروپا به ’قرون تاریک‘ معروف است آنقدها هم تاریک
نبود، و در آن زمان پیشرفتهای اندکی نیز در اروپا صورت میگرفت.
پیشرفتهای چینیها خیره کننده بودند. تا همین اواخر، بیشتر تاریخنگارانِ
ریاضی یک رویکرد اروپایی را اتخاذ میکردند و توجه زیادی به خاور دور نداشتند. این
رویکرد تا زمانی که George Gheverghese Joseph در سال 1991 کتاب تاجِ
طاووس (The Crest of the Peacock) را نوشت ادامه داشت. این کتاب درباره تاریخ ابتدایی ریاضیات در
خاور دور است. یکی از ریاضیدانانِ بزرگِ چینِ باستان کسی بود بنام لیو هوی (Liu Hui).
او یکی از اشرفزادگان ژیانگ از خاندان هان (Han)
بود، که دوران سهپادشاهی در استان کائووی میزیست. او در سال 263 کتابی را منتشر
کرد که حاوی حل مسائلی بود که در کتابِ معروفِ ریاضیدان چینی جیوژنگ سوانشو
(Jiuzhang Suanshu)، با عنوان ’ ُنه فصل درباره هنر ریاضی‘، آمده بودند.
از میان کارهایش میتوان به اینها اشاره کرد: اثبات قضیه فیثاغورث، اثبات
قضایایی در هندسه فضایی، بهبود تخمین ارشمیدس برای عدد π، و یک روش نظاممند برای حل معادلات خطی چند مجهوله. او همچنین
مطالبی درباره نقشهبرداری، نوشت که کاربردهای خاصی در نجوم داشتند. او احتمالاً
از شهر لویانگ (Luoyang)، که یکی از چهار پایتخت چین باستان بود، دیدن کرده، و سایه
خورشید را اندازه گرفته بود.
![]()
اولین شواهدی که برای تاریخ اولیه چین وجود دارد از متون جدیدتری سرچشمه میگیرند،
چیزهایی مثل سوابق تاریخ کبیر (حوالی سال 110 ق.م)، و سالنامههای
خیزرانی، که بر روی تکههایی از چوب خیزران نوشته و در سال 296 در مقبره شاه شیانگ
دفن شد و در سال 281 ب.م کشف شدند. بر طبق این متون، تمدن چین در هزاره سوم
پیش از میلاد با سلسله شیا (Xia) آغاز میشود. سوابق مکتوب با سلسله شنگ آغاز میشود که در حوالی
سالهای 1600 تا 1046 ق.م حکمرانی میکردند، و همینها بودند که اولین سوابق شمارش
چینی، که بصورت استخوانهای پیشگو[1]
بودند، را از خودشان بجا گذاشتند. هنگامی که سلسله ژو (Zhou) بر
چین مسلط شد، در اثر پیدایش ساختارهای ملوکالطوایفی این کشور پایدارتر شد. این
وضعیت سه قرن ادامه داشت تا اینکه چین توسط گروههای دیگری از هم جدا شد.
تا سال 476 ق.م نوعی هرج و مرج بر چین حاکم بود، دورانی که به جنگ ایالات
معروف بود و بیش از دو قرن طول کشید. کتاب ژو بی نیز در طول همین دوران
پرتلاطم نوشته شد. محتوای اصلی ریاضی این کتاب چیزهای هستند که حالا به اسامی
دیگری شناخته میشوند، چیزهایی مثل قضیه فیثاغورث، کسور، و حساب. این کتاب همچنین
شامل مقدار زیادی از مطالب نجومی است. قضیه فیثاغورث بصورت گفتگویی که میان دو
اشراف زاده در جریان است مطرح میشود. گفتگوی آنها درباره مثلثهای قائمالزاویه
به فرمول معروف این قضیه، و اثبات هندسی آن منجر میشود. برای مدتی تاریخنگاران
تصور میکردند که این کشف چینیها با اختلاف پانصد سال از فیثاغورث جلوتر است. ولی
امروزه دیدگاه عمومی بر این است که این کشف مستقلی بوده، که زودتر از فیثاغورث
صورت گرفته، ولی فاصله چندانی هم با آن نداشته.
یکی از آثار مهم همان دوره ’ ُنه فصل درباره هنر ریاضی‘، است که قبلاً
به آن اشاره شد، و حاوی مطالب متنوعی مثل استخراج ریشهها، حل معادلات چند مجهوله،
بدست آوردن سطح و حجم، و مثلثهای قائمالزاویه بود. ریاضیدان چینی چانگ چنگ در
سال 130 ب.م در حواشی که بر این کتاب نوشته، تخمینی برای مقدار ![]() آمده است. حواشی دیگری که توسط چائو چون در حوالی قرن سوم
میلادی نوشته شده روشی برای حل معادله درجه دوم را بدست میدهد. مهمترین پیشرفتی که در این کتاب بوجود آمد از سوی
بزرگترین ریاضیدان چینی عهد باستان، یعنی لیو هوی، در سال 263 ب.م حاصل شد. او در
مقدمه این کتاب شرح میدهد:
آمده است. حواشی دیگری که توسط چائو چون در حوالی قرن سوم
میلادی نوشته شده روشی برای حل معادله درجه دوم را بدست میدهد. مهمترین پیشرفتی که در این کتاب بوجود آمد از سوی
بزرگترین ریاضیدان چینی عهد باستان، یعنی لیو هوی، در سال 263 ب.م حاصل شد. او در
مقدمه این کتاب شرح میدهد:
در گذشته سلطان ستمگری بنام کوین، آثار نوشته شده را آتش زد، که این به
نابودی دانش گذشتگان منجر شد. بعدها ژنگ کنگ و جنگ شوچانگ که به
دلیل قدرتی که در انجام محاسبات داشتند معروف بودند، تصمیم گرفتند متونِ باستانیِ
نابود شده را احیاء کنند. ژنگ کنگ و تیم او نسخههای جدیدی را درست کردند که قسمتهای بیکیفیت از آنها جدا، و جای آنها پر شده بود. بنابراین
آنها قسمتهایی را اصلاح کردند، و نتیجه این شد که اینها با قسمتهای قدیمی فرق داشتند.
کاری که لیو هوی بویژه انجا میداد،
ارائه اثبات برای روشهایی بود که در کتاب آمده
بودند. گرچه این اثباتها مانند آنچه که ارشمیدس
در کتاب روش خود آورده بود، آنقدرها دقیق و محکم نبودند.
![]()
اولین فصل کتاب ُنه فصل به شرح چگونگی محاسبه مساحتهای اشکال مختلف، مانند چهارگوش، مثلث،
ذوذنقه، و دایره میپردازد. قواعدی که در این کتاب ارائه میشود، به جزء مورد دایره، صحیح هستند. حتی در این حالت نیز
دستورالعمل صحیح است: شعاع را در نصف محیط ضرب کنید تا مساحت دایره بدست آید. ولی
محاسبه محیط بعنوان 3 برابر قطر آن مطرح شده، که در عمل π را مساوی 3 قرار میدهد.
اگر از این قاعده استفاده شود، مساحت را به میزان 5 درصد کمتر برآورد میکند.
در اواخر صده نخست پیش از میلاد، حاکمی بنام ونگ منگ به منجم و تقویمنگار چینی لیو هسینگ دستور داد تا روش استانداردی
برای اندازهگیری حجم پیدا کند. لیو
هسینگ یک آوند استوانهای شکل بسیار دقیق برونزی ساخت که از آن بعنوان یک اندازهگیری
مرجع استفاده میکرد. هزران کپی از این استوانه ساخته شده، و در سراسر چین مورد
استفاده قرار میگرفت. حالا آوند اولیه در موزهای در پکن نگاهداری میشود، و
ابعاد آن به این دلالت دارند که مقداری که لیو هسینگ برای عدد π درنظر گرفته بود چیزی در حدود 3.1547 بود. در
کتاب تاریخ سلسله سویی (Sui) مطلبی نقل شده که معادل یافته لیو هسینگ برای عدد π است. در حول و حوش همان زمان، لیو هوی که طالعبین دربار چنگ
هنگ بود، پیشنهاد داد که مقدار π ریشه دوم 10 باشد، یعنی
چیزی حدود 3.1622. روشن بود که تخمینهایی که برای π پیشنهاد میشد در حال
بهبود بود.
لیو هوی، در حواشی که بر کتاب ’نه فصل‘ نوشت به این نکته اشاره کرد که مقدار
سنتی ’ π=3‘ اشتباه
است، این مقدار بجای اینکه محیط دایره را بدهد، محیط یک چندضلعی محاط شده در
دایره را میدهد، که به وضوح مقدار کوچکتری است. سپس او مقدار دقیقتری را برای
محیط دایره حساب کرد (که بطور ضمنی تخمین جدیدی را برای π نیز بدست میداد). در واقع او جلوتر رفت و یک روش محاسباتی برای
برآورد π ارائه داد که میتوانست مقدار آن را
با هر دقتی محاسبه کند. رویکرد او شبیه به روشی بود که ارشمیدس از آن استفاده میکرد،
یعنی تخمین محیط دایره توسط چندضلعیهای منظم 6, 12, 24, 48, 96 …
ضلعی. ارشمیدس به منظور بکارگری روش افنا از یک سری از تخمینها که بر اساس
چندضلعیهای محاط در دایره بودند، و همچنین از یک سری دیگر از تخمینها که براساس
چندضلعیهای محیط بر دایره بودند، استفاده کرد. لیو هوی تنها از چندضلعیهای محاط
در دایره بودند استفاده کرد، ولی او در انتهای محاسبه خودش یک استدلال هندسی را
ارائه میدهد که حد پایینی و بالایی مقدار صحیح π را تعیین میکند. این روش، با استفاده از محاسباتی که سختتر از
جذر گرفتن نبود، تخمین صحیحی را برای π
بدست میداد، و تا هر رقم دلخواه میشد آن را ادامه داد. این محاسبات نظاممند
بودند، و نسبت به محاسبهِ یک حاصلضربِ طولانی، دشوارتر نبودند. یک حسابگر خبره در
عرض یک روز میتوانست تا ده رقم اعشارِ عدد π را حساب کند.
بعدها در حدود سال 469 ب.م، ریاضیدانی بنام زو چونگ چی (Tsu Ch’ung Chih)
این محاسبات را گسترش داد و نشان داد که
3 · 1415926 < π < 3 ·
1415927
این نتیجه در تاریخ ثبت شد، ولی روش او، که روشهای درونیابی (Interpolation) نام داشت، مفقود شد. این روش میتوانست ادامهِ محاسبات لیو هوی باشد، ولی عنوان کتاب او حاکی از برآورد مقادیر دقیقتری بود که بر اساس یک جفت از برآوردهای قبلی، که یکی خیلی کوچک و دیگری خیلی بزرگتر بود، حاصل میشدند. حالا روشهایی شبیه به این بطور گسترده در ریاضیات مورد استفاده قرار میگیرند. حتی تا چند دهه پیش آنها را در مدارس به دانشآموزان یاد میدادند. زو (Tsu) برای تخمین π به دو کسر ساده دست یافت، یکی کسر ارشمیدس، یعنی 22/7، که مقدار π را تا دو رقم بدست میداد، و دیگری کسر 355/113، بود که مقدار π را تا شش رقم اعشار بدست میداد. امروز از کسر اول بطور گسترده استفاده میشود، و دومی بیشتر برای ریاضیدانان شناخته شده است.
![]()
یکی از اثباتهای که درباره قضیه فیثاغورث ارائه شد، توسط لیو هوی انجام گرفت،
و بر اساس دستوراتی است که در کتاب خودش آورده و حالتی نبوغآمیز دارد. مثلث قائمالزاویه
به رنگ سیاه نشان داده شده. مربعی که در یکی از اضلاع قرار دارد (پایینی) توسط قطر
خودش به دو قسمت تقسیم شده. مربع دیگری که بر یکی دیگر از اظلاع قرار دارد به پنج
قسمت تقسیم شده: یک مربع کوچک (خاکستری تیره)، یک جفت مثلث که بطور متقارن چیده
شدهاند و اندازه آنها با ضلع مثلث اولیه یکی است (خاکستری متوسط) و یک جفت مثلث
متقارن و یک شکل که بقیه فضا را پوشاندهاند (سفید). سپس کلیه هفت قطعه روی هم
گذاشته میشوند تا مربعی را پر کنند که ضلع آن به اندازه وتر مثلث است.
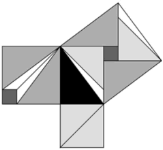
اثبات لیو هوی برای قضیه
فیثاغورث.
ریاضیدانان چین باستان به اندازه همتایان یونانی خودشان لایق بودند، والبته
بعد از دوره لیو هوی، چین شاهد کشفیات بسیاری در حوزه ریاضیات بود، که نسبت به
ریاضیات اروپا تقدم داشت. برای مثال، تخمینهایی که توسط لیو هوی و زو چونگ برای
محاسبه عدد π ابداع شدند،
تا هزار سال بعد از آنها کارآمد بود.
جوزف به بررسی این موضوع میپردازد که شاید ایدههای ریاضیدانان چینی از طریق
مراودات تجاری به هند و خاورمیانه منتقل شده و از آنجا به اروپا راه یافته. اگر
چنین باشد، ممکن است اکتشافاتی که بعداً در اروپا انجام گرفت کاملاً مستقل نباشند.
از قرن ششم میلادی دیپلماتهای چینی در هند حضور داشتند، و کتابهای ریاضی و ستارهشناسی
هندی در قرن هفتم به زبان چینی ترجمه شدند. تا جایی که به کشورهای اسلامی مربوط
است، از پیامبر اسلام حدیثی هست که میگوید ’بدنبال دانش باشید، حتی اگر در چین
باشد.‘ در سفرنامههایی که در قرن چهاردهم میلادی از مسافرین عرب بجا مانده گزارشهایی
از ارتباطات تجاری با چین هست. سیاح و ادیب مراکشی محمد ابنبطوطه در
سفرنامه خودش بنام الرحلة (به معنای سفر)، درباره علم، تکنولوژی و
فرهنگ چینیها مطالبی زیادی را نوشته.
همانطور که دو فصل بعدی این کتاب نشان خواهد داد، ما میدانیم که ایدههای
زیادی از هند و سرزمینهای اسلامی راه خودشان را به اروپای قرون وسطی باز کردند.
بنابراین از هر جهتی غیر ممکن نیست که در مورد علوم چینی نیز چنین باشد. حضور
کشیشان مسیحی در قرون هفده و هجده در چین موجب الهام لایبنیتز از کنفسیوس شد.
ممکن است شبکه پیچیدهای برای انتقال ریاضیات، علوم، و موارد دیگر میان یونان،
خاورمیانه، هند، و چین وجود داشته. و اگر چنین بوده، ممکن است تاریخِ متداولِ ریاضیات
به تجدید نظرهایی نیاز داشته باشد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

محمد بن موسی خوارزمی : تولد: حوالی سال 780
میلادی، وفات: حدود 850 میلادی.
بعد از
وفات پیامبر اسلام در سال 632 میلادی، کنترل جهان اسلام به خلفای متعددی رسید. اصولاً این
خلفا بر اساس شایستگیشان برگزیده میشدند، بنابراین سیستم خلافت اسلامی صرفاً یک
نظام سلطنتی نبود. ولی، خلیفه مسئول اصلی بود. در سال 654 میلادی، در زمان خلیفه
سوم، که عثمان نام داشت، خلافت اسلامی به بزرگترین امپراتوری بدل شد که جهان تا آن
زمان به خود دیده بود. گستره جغرافیایی آن شامل شبهجزیره عربستان، شمال آفریقا از
مصر گرفته تا لیبی و تونس، خاور نزدیک، قفقاز، و بیشتر آسیای مرکزی از ایران گرفته
تا پاکستان، افغانستان، و ترکمنستان را شامل میشد.
پس از چهار خلیفه اول، که خلفای راشدین نامیده میشدند، سلسله بنیامیه روی
کار آمد، که آنها نیز توسط خاندان عباسی و با کمک ایرانیان سرنگون شدند. حکومت
مرکزی، که ابتدا در دمشق قرار داشت، به بغداد منتقل شد. این شهر در سال 762 میلادی
توسط خلیفه عباسی المنصور بنیان نهاده شد. بغداد، که محل آن به ایران نزدیک بود،
بواسطه نیازهای خودش، ابتدا با خدماتی که مدیران ایرانی ارائه میدادند اداره میشد.
آنها بخوبی از تعامل سرزمینهای مختلف امپراتوری اسلامی آگاه بودند. به همین جهت،
مقام وزیر ایجاد شد، و این به خلیفه اجازه میداد تا کارهای اجرایی را بر
عهده وزیر بگذارد. از سوی دیگر، خود وزیر نیز امور محلی را به عهده امیران آن
نواحی میسپرد. کمکم قدرت واقعی در دستان وزیران (عمدتاً ایرانی) قرار گرفت، و
مقام خلافت قدرت خودش را از دست داد. ولی در ابتدای خلافت عباسیان، خلیفه کنترل
زیادی را اعمال میکرد.
هارونالرشید در حدود سال 800 میلادی بیتالحِكمَة را تاسیس کرد، که کتابخانهای
بود که در آن کتابهایی از فرهنگهای دیگر به زبان عربی ترجمه میشدند. این پروژه
توسط پسرِ هارونالرشید، یعنی مأمون، به انجام رسید، و مجموعه عظیمی از کتابهای
یونانی به عربی ترجمه شد. بغداد به مرکز علم و بازرگانی تبدیل شد، و دانشمندان و
تُجار سراسر جهان، حتی از مکانهای دوری مثل چین و هند نیز، به بغداد میآمدند. از
جمله این دانشمندان محمد بن موسی خوارزمی بود، که در تاریخِ ریاضیات نقش
عمدهای دارد.
خوارزمی در آسیای میانه، در شهری بدنیا آمد که آن زمان خوارزم نامیده میشد و
حالا خیوه نام دارد و در اُزبکستان کنونی واقع شده. او عمده کارهایش را در زمان
خلافت مأمون انجام داد. او کمک کرد تا دانشی که از یونانیان بجا مانده و بسرعت در
حال کمرنگ شدن بود، زنده نگاه داشته شود. او کُتب خطی مهم یونانی و هندی را ترجمه
کرد، و خودش مطالبی را به آنها افزود و بانی پیشرفتهایی در علوم، ریاضیات، نجوم،
و جغرافیا شد. او همچنین چندین کتاب نوشت که شبیه کتابهای پرفروش امروزی بود. از
میان آنها، در حوالی سال 825 میلادی، خوارزمی کتاب ’ الجمع و التفريق في الحساب
الهندي‘ یا حساب با اعداد هندی را نوشت. بعدها این کتاب تحت عنوان ’Algoritmi de Numero Indorum‘ به
لاتین ترجمه شد و موجب گشت تا این روش محاسبه جدید در اروپای قرون وسطی گسترش
یاید. در عین حال، نام این کتاب از Algoritmi به Algorismi
تغییر یافت، و روشهای محاسبه با این اعداد (اعداد هندی) الگوریسم (algorism)
نامیده شدند. بعداً در قرن هجدهم این لغت به الگوریتم (algorithm) تغییر نام
داد.
کتاب او با نام ’ المختصر فی حساب و الجبر و المقابله‘ در
حوالی سال 830 نگاشته شد، این کتاب در قرن دوازده میلادی توسط روبرت چستر به لاتین
ترجمه شد. عنوان لاتین آن ’Liber Algebrae et Almucabola ‘ بود که به معنای ’کتاب جبر و مقابله‘ است. در
نتیجه، لغت عربی الجبر به لغت لاتین algebra تبدیل شد، و از آن زمان به بعد نیز این لغت پابرجا بوده. حالا علم
جبر بر استفاده از علائمی مانند x و y
بجای کمیتهای مجهول، و همچنین روشهایی برای یافتن این مجهولات توسط حل معادلات
اشاره دارد. ولی در کتاب اصلی خوارزمی از علائم استفاده نشده بود.
![]()
کتاب جبر و مقابله در زمانی نوشته شد که خلیفه مأمون خوارزمی را تشویق
کرد تا کتاب سادهای درباره محاسبه بنویسد. خوارزمی هدف از نوشتن این کتاب را چنین
شرح میدهد:
سادهترین و مفیدترین راهی که بتوان از آن در اموری که انسان دائماً به آنها
نیاز دارد، مثل ارث و میراث، تقسیم اراضی، اندازه گیری اراضی، دعاوی حقوقی، تجارت،
محاسبات هندسی، و موارد مشابه دیگر استفاده کرد در حساب چیست؟
چنین مواردی شباهت زیادی به جبر ندارند. در واقع مطالبی که در کتاب مذکور
درباره جبر آمده بخش اندکی را تشکیل میدهد. خوارزمی میگوید ’بطور کلی من دریافتهام
که آنچه مردم میخواهند محاسبه کنند، همیشه یک عدد است‘، سپس بر این اساس، با سادهترین
بیان شروع به توضیح اعداد میکند (یکان، دهگان، صدگان). این کتاب رسالهای
نبود که مختص دانشمندان باشد، بلکه یک کتاب عامه فهم ریاضی بود، نوعی کتاب درسی که
مخاطب آن خواننده عام بود. این چیزی بود که خلیفه میخواست، و همان چیزی بود که به
او تقدیم شد. خوارزمی کتاب خودش را به این عنوان در نظر نمیگرفت که در آن مطالبی
در مورد آخرین پیشرفتهای ریاضی مطرح شده باشد. ولی ما حالا بخشی که مربوط به جبر
بود را بعنوان یکی از موارد پیشرفته آن زمان در نظر میگیریم. این عمیقترین بخش
کتاب بود که در آن روشهایی برای حل معادلات و بدست آوردن مجهولات مطرح میشود.
معمولاً لغت جبر بعنوان ’تکمیل‘ ترجمه میشد، و به جمع جملات یکسان در
طرفین معادله به منظور ساده کردن آن دلالت دارد. لغت مقابله به ’متعادل
کردن‘ ترجمه میشود، و به انتقال یک جمله از یک سمت معادله به سمت دیگر (البته با
علامت مخالف)، و حذف جملات یکسان در طرفین معادله دلالت دارد.
اگر بخواهیم یک معادله را به صورت نمادگذاری امروزی مطرح کنیم، مثلاً میتوانیم
آن را بصورت زیر بنویسیم:
x − 3 = 7
دراینصورت جبر به ما اجازه میدهد تا به طرفین معادله 3 را
اضافه کنیم تا به معادله زیر برسیم:
x = 10
که در اینحالت معادله حل شده و جواب آن مشخص است. اگر معادله بصورت زیر باشد:
2x2 + x
+ 6 = x2 + 18
آنگاه مقابله به ما اجازه میدهد 6 را از سمت
چپ به سمت راست منتقل کنیم، و چون در سمت راست علامت آن تغییر میکند آن را از 18 کم
میکنیم تا به معادله زیر برسیم
2x2 + x
= x2 + 12
مقابله دوم به ما اجازه میدهد تا جمله x2 را از سمت راست به سمت چپ انتقال دهیم
و چون علامت آن تغییر کرده، آن را از2x2 کم
کنیم تا به معادله زیر برسیم
x2 + x = 12
که گرچه جواب آن هنوز مشخص نیست، ولی نسبت به معادله اولیه سادهتر است.
دوباره تاکید میکنم که خوارزمی از علائم استفاده نمیکرد. در واقع پدرِ جبر
آنچه را که بیشتر ما حالا آن را بعنوان جبر در نظر داریم انجام نمیداد. او همه
چیز را بطور شفاهی بیان میکرد. اعدادِ خاص، واحد نام داشتند، کمیت مجهولی
که حالا ما آن را به نام x میشناسیم، آن موقع ریشه
نام داشت، و x2 هم مربع. مطابق با این اصطلاحات، بدون اینکه از هیچ علامتی
استفاده شود، معادله فوق اینطور خوانده میشد:
مربع بعلاوه ریشه مساوی دوازده واحد.
بنابراین قدم بعدی این بود که چگونه از چنین معادلهای به جواب دست پیدا کنیم.
خوارزمی معادلات را به شش نوع تقسیم بندی کرد، که یکی از آنها ’مربع بعلاوه ریشه
مساوی واحدها‘ بود، درست مثل معادله x2 + x = 12 .
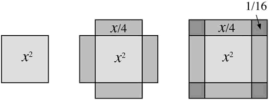
حل هندسی معادلاتی که
خوارزمی آنها را ’مربع بعلاوه ریشه مساوی واحدها‘ مینامید.
سپس او به تحلیل هر یک از انواع این معادلات پرداخت، و آنها را توسط مخلوطی از
روشهای جبری و هندسی حل کرد. بنابراین خوارزمی برای حل معادله x2 + x
= 12 مربعی را رسم میکرد که نمایانگر x2 بود
(شکل بالا سمت چپ). برای اضافه کردن x او چهار مستطیل را به هم
متصل میکرد، که طول هر یک از اضلاع آنها x و ¼ بود (شکل بالا وسط). در نتیجه
شکلی که حاصل میشد به این ایده منجر میشد که با اضافه کردن چهار مربع کوچک، که
طول ضلع هر یک از آنها ¼ و مساحت آنها 1/16 بود، مربع
بزرگتر تکمیل شود. بنابراین او ¼ = 4× 1/16 را به سمت چپ معادله اضافه کرد (شکل بالا سمت راست). بر طبق
قاعده جبر، او باید ¼ را به سمت راست معادله
نیز اضافه میکرد، که با اینکار حالا این عدد به ¼12 تبدیل میشد.
(x+ 1/2)2
= 12¼ = 49/4 = (7/2)2
که با جذر گرفتن از طرفین خواهیم داشت:
x+ 1/2 = 7/2
بنابراین x = 3 خواهد بود. امروزه ما اعداد منفی را نیز بعنوان جذر
یک عدد مثبت قبول داریم، بنابراین معادله زیر نیز قابل قبول است
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF کتاب را
تهیه کنید.

مدهاوا (Madhava): تولد: حوالی سال 1350
میلادی هند، وفات: حدود 1425 میلادی.
اگر
خبرهای هواشناسی را دنبال کرده باشید، شاید این خبر را شنیدهاید که میگوید ”وزن آبهای
طوفان ریتا (Rita) به
اندازه 100 میلیون فیل است“. امروزه در برخی از رسانهها از فیل بعنوان واحد وزن
استفاده میشود، همچنین از بلژیک و ولز بعنوان واحد مساحت، از استخرهای المپیک
بعنوان واحد حجم، و از اتوبوسهای لندن برای طول و ارتفاع استفاده میشود. بر این
اساس، شما از پاراگراف زیر چه برداشتی میکنید؟
(33) خدا، (2) چشم، (8) فیل، (8) مار، (3) آتش، (4) ودا، (27) ناکساتراس ، و
(2) بازو – درست است که بگویم این اندازه محیط دایرهای است که قطر آن 900000000000
باشد.
چیزی به نظرتان میآید؟ در واقع این ترجمه شعری است که در سال 1400 میلادی
توسط مادهاوا سانگاماگراما (Madhava of Sangamagrama)
درباره عدد π نگاشته شده.
احتمالاً مادهاوا بزرگترین ریاضیدان و منجم هندی قرون وسطی بود. خدایان، فیلها،
مارها، و غیره، نماد اعداد هستند که بعنوان کاغذ کوچکی ترسیم شدهاند. آنها بطور
جمعی نشاندهنده عدد زیر هستند:
282, 743, 388, 233
که اگر آن را بر 900 میلیارد تقسیم کنیم عدد زیر حاصل میشود:
3·141592653592222…
این عدد باید آشنا باشد. نسبت اشاره شده تعریف عدد π است، که مقدار دقیقتر آن عبارت است از:
3·141592653589793…
دو عدد اشاره شده تا 11 رقم اعشار با هم توافق دارند. تا آن زمان، این یکی از
بهترین تخمینهایی بود که برای عدد π بدست آمده بود. در سال 1430 میلادی، ریاضیدان ایرانی غیاثالدین
جمشید کاشانی در کتاب مفتاحالحساب این رکورد را شکست و عدد π را تا 16 رقم اعشار برآورد کرد.
برخی از آثار نجومی مادهاوا باقی ماندهاند، ولی کارهای ریاضی او فقط از طریق
روایتهای بعدی بدست ما رسیده. مشکل همیشگی دادن اعتبار به شخصیتهای مهم و
استادان (مثلاً قضیه فیثاغورث که توسط یکی از اعضای فرقه فیثاغورثیان کشف شد، ولی
اعتبار آن به خود فیثاغورث نسبت داده میشود) به این معنی است که ما دقیقاً نمیتوانیم
مطمئن باشیم این قضایا توسط خود مادهاوا کشف شدهاند یا نه. بر این اساس، من فرض
را بر این میگیرم که سخن اخلاف او درست است.
بزرگترین دستآورد او معرفی دنبالههای نامتناهی بود، که به معنای برداشتن
اولین قدمها در راه آنالیز ریاضی بود. او چیزی را کشف کرد که در جهان غرب به دنباله
گریگوری برای تابع معکوس تانژانت معروف است، و به عباراتی نامتناهی برای
محاسبه π میانجامد.
شکوهمندترین کشفیات او عبارتند از دنبالههای نامتناهی برای توابع مثلثاتی سینوس
و کسینوس، که بعداً در جهان غرب بیش از دویست سال بعد از او دوباره توسط نیوتون
کشف شدند.
![]()
اطلاعات اندکی از زندگی مادهاوا در دست است. او در دهکده سانگاماگراما بدنیا
آمد، و به همین دلیل نیز به مادهاوای سانگاماگرامای شناخته میشود تا از
مادهاواهای دیگر، مثل ویدیا مادهاوا که طالع بین معروفی بود متمایز شود.
دهکده سانگاماگراما دارای معبدی نیز بود که به خدایی به همین نام وقف شده بود.
تصور میشود که مکان فعلی این دهکده در جایی نزدیک دهکده براهمین در ایالت کرالا
کنونی باشد. در اواخر قرون وسطی کرالا خاستگاه تحقیقات ریاضی بود. بیشتر
ریاضیدانان پیشین هند از ایالات شمالی میآمدند، ولی به دلایل ناشناخته، کرالا
دستخوش نوعی جهش فرهنگی شد. بطور کلی ریاضیات در هند باستان بعنوان شاخهای از علم
نجوم شناخته میشد، و مادهاوا مدرسه نجوم و ریاضیات کرالا را تاسیس کرد.
این شامل تعدادی از ریاضیدانان بسیار زبردست میشد. از میان آنها میتوان به
منجم هندی پارامشوارا (Parameshvara) اشاره کرد، که از رسد گرفتگیها برای بررسی درستی روشهای
محاسباتی استفاده میکرد. او حداقل 25 رساله نوشت. منجم دیگری بنام (Kelallur Nilakantha Somayaji) در سال 1501 یک رساله برجسته بنام تانتراسامگراها (Tantrasamgraha) در
حوزه نجوم نگاشت، که شامل 432 متن سانسکریت بود که در هشت فصل به نظم درآمده بود.
این اثر به ویژه شامل اصلاحاتی بود که او در کارهای ریاضیدان و منجم بزرگ هندی آریابهاتا (Aryabhata)
درباره نظریه حرکت مریخ و زهره انجام داده بود. او همچنین تفسیرهای جامعی درباره
کارهای دیگر آریابهاتا نوشت که شامل جبر، مثلثات، و دنبالههای نامتناهی برای
توابع مثلثاتی بود. ریاضیدان دیگری بنام جیِستادوا (Jyesthadeva)
کتابی بنام یوکتیباهاسا نوشت که تفسیری بر تانتراسامگراها بود و در
آن اثباتهایی برای قواعد اصلی آن اضافه شده بود. برخی از این کتاب بعنوان اولین
متن حسابان یاد میکنند.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

جرلامو کاردانو (Girolamo Cardano): تولد: 1501 میلادی میلان
ایتالیا. وفات: 1576.
”من از اوان جوانی خودم برای فراگیری شمشیربازی تلاش فراوانی کردم، تا
آنکه بواسطه تمرینات مداوم توانستم حتی در میان استادان این فن نیز جایگاهی کسب
کنم ... شب هنگام، برخلاف لباس اشرافی که به تن داشتم، خود را مسلح میکردم و در
اطراف شهرهایی که در آنها منزل گزیده بودم پرسه میزدم ... روپوشی از ابریشم سیاه
به تن میکردم تا ظاهرم را بپوشاند، کفشهایی از پشم گوسفند بپا میکردم ... و اغلب
شبها سرگردان بودم تا صبح بسر رسد.“
این توصیفی است که میتوان از زندگی ایتالیای دوران رُنسانس در حوالی سال 1520
ارائه داد - یا حداقل برای جرلامو کاردانو (Girolamo Cardano) که چنین
چیزهایی را زندگینامه خودش توصیف میکند، زندگی اینطور بود. کاردانو علامهای
بود که خصوصاً در ریاضیات و پزشکی استعداد فراوانی داشت. بدلیل اینکه کاردانو
اعتیاد شدیدی به قمار داشت، او میراث خانوادگیاش را بر باد داد، و در یک خانه
محقر و ویران زندگی میکرد. وقتی به قمارباز دیگری شک کرد که تقلب میکند، به صورت
او چاقو زد. او به کفر گویی متهم و و روانه زندان شد. پسرش به جرم مسموم کردن
همسرش اعدام شد. ولی کاردانو زبان اُسقف سنت اندرو، که مدتها لال شده بود، را گشود
و برای اینکار 1400 سکه پاداش گرفت. او که حالا با یک پیروزی به ایتالیا بازگشته
بود در کالج اطباء پذیرفته شد، جایی که برای مدتها از پذیرفتن او طفره میرفتند.
مهمتر از همه، او یک استاد ریاضی بود که یکی از برجستهترین کتابهای تاریخ
ریاضیات، یعنی هنر والا (Ars Magna) را نوشته بود. عنوان فرعی این کتاب قواعد جبر بود. در کتاب هنر
والا، جبر از شکل سنتی خودش خارج شد، و در آن عبارات نظاممند، و بشکل علامتگذاری
شده بیان شدند. در این مرحله، از کاردانو میشد بعنوان نامزد دیگری برای ’پدر جبر‘
نام برد. گرچه این مورد تا اندازهای صحیح بود، ولی او این عنوان را راحت و بدون
مناقشه کسب نکرد.
![]()
کاردانو یک فرزند نامشروع بود. پدرش فازیو، وکیلی بود که در ریاضی استعداد
فراوانی داشت. او مردی بود که خلق و خوی ظریفی داشت، و در شهر پاویا (Pavia)
زندگی میکرد و دوست لئوناردو دا وینچی بود. او عادت داشت یک عبای ارغوانی
نامعمول بپوشد و یک عرقچین سیاه کوچک بر سرش بگذارد، و همه دندانهایش را در سن
55 سالگی از دست داد. کییارا، مادر جرلامو بیوهزن جوانی بود که از قبل سه
فرزند داشت، و بعد از بدنیا آمدن او با پدرش ازدواج کرد. او زن فربهای بود که خلق
و خویی شبیه به فازیو داشت، و سریعاً حالت تهاجمی میگرفت. او همچنین خیلی مذهبی و
خیلی باهوش بود. هنگامی که او جرلامو را حامله بود، در میلان طاعون شیوع پیدا کرده
بود، و بهمین دلیل او به دهات اطراف رفت تا از بلا به دور بماند. این در حالی بود
که سه فرزند قبلیش در شهر ماندند و نهایتاً از طاعون تلف شدند. قدم این نو رسیده
خیلی مایه مسرت نشد. او در کتاب زندگینامه خود مینویسد ” هرچند داروهای مختلفی
برای سقطجنین به مادرم داده بودند ...، ولی با اینحال من در 24 سپتامبر سال 1500
بطور عادی بدنیا آمدم.“
گرچه شغل فازیو وکالت بود، ولی آنقدر در ریاضیات مهارت داشت تا به داوینچی
درمورد مسائل هندسی مشاوره بدهد، او همچنین در دانشگاه پاویا هندسه درس میداد.
او این مهارتهای ریاضی و طالعبینی را به پسر حرامزاده خودش یاد داد. کاردانو
نقل میکند ”پدرم در اوان کودکیم به من اصول حساب را یاد داد، و در همان زمان من
را با علوم غریبه آشنا ساخت ... به من اساس طالعبینی عربی را یا داد ...
هنگامی که به دوازده سالگی رسیدم، او شش جلد اول کتاب اصول اقلیدس را به من
آموخت.“
جرلامو کودکِ بیماری بود، و تلاشهای پدرش که قصد داشت او را به حرفه حقوق
وارد کند با شکست روبرو شد. او که بعنوان یک دانشجوی پزشکی در دانشگاه پاویا ثبتنام
کرده بود، استعداد درخشان خودش را نشان داد، و گرچه خیلیها رکگوییهای او را
توهینآمیز میدیدند، ولی او با اختلاف یک رای بعنوان رئیس انتخابی دانشگاه
برگزیده شد. موفقیت در جلو او قرار داشت. در همین زمان بود که درحالی که به شمشیر
مسلح بود، شبها در خیابانهای شهر پرسه میزد، و در همین زمان بود که به قمار روی
آورد. فهم کاردانو از ریاضیاتِ شانس، به او مزیت خاصی میداد، چیزی که باعث شد
نهایتاً در سال 1564 او یکی از اولین کتابهای مربوط به احتمالات را بنویسد. نام
این اثر ’کتابِ بازی شانس‘ بود، که صدسال بعد در سال 1663 منتشر شد.
توانایی او در بازی شطرنج (برای پول) نیز برای او مفید بود. ولی هر چه زمان میگذشت،
او بداخلاقتر و فاسدتر میشد، او بختِ خود، و همچنین میراث خانوادگیاش را از دست
داد.
با اینحال او کارش را ادامه داد. حال که یک مدرک پزشکی بدست آورده بود، تلاش
کرد تا به کالج اطباءِ میلان وارد شود، یعنی جایی که دروازه یک زندگی پرمنفعت بود
و میتوانست تا آخر عمر راحت زندگی کند. در این زمان رکگویی و صراحتی که در بیان
افکارش داشت باعث شد تا نزول کند، و به همین دلیل او را به کالج اطباء راه ندادند،
و او مجبور شد بعنوان یک دکتر عادی در یکی از دهات اطراف کار کند. این فقط خرج یک
زندگی بخور و نمیر را برای او تامین میکرد، و در همین زمان بود که او با دختر یک
افسر ارتش بنام لوسیا باندارینی ازدواج کرد. او که دوباره از ورود به کالج
محروم شده بود به شغل قبلی خودش، یعنی قمار، روی آورد و ثروت هنگفتی را از دست
داد. پس از اینکه او کلیه داراییهای خانوادگی، از جمله جواهرات لوسیا، را از دست
داد، آنها مجبور شدند به یک خانه محقر نقل مکان کنند. کاردانو مینویسد ’من خودم
را تباه کردم! نابود شدم!‘ او و لوسیا فرزندی داشتند که از نقصهای متعددی رنج میبرد،
ولی در آن زمان چنین بچههایی نادر نبودند. حالا پدرش فازیو مرده بود، و جرلامو
بعنوان جانشین او منسوب شده بود. سرانجام زندگی شروع به خوب شدن کرد. حتی در سال
1539 کالج اطباء نیز دیگر از ورود او ممانعت نکرد. او حالا با انتشار تعداد زیادی
از کُتب ریاضی، چیزهای دیگری را هم به زندگی حرفهای خودش وارد کرده بود. انتشار
یکی از این کتابها باعث شد جای پای او بعنوان یکی از برجستهترین ریاضیدانان
تاریخ تثبیت شود.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

پییر دو فرما (Pierre de Fermat): تولد: 1601 میلادی فرانسه.
وفات: 1665.
تعداد
قلیلی از ریاضیدانان هستند که
مسئلهای را طرح کرده باشند که برای قرنها لاینحل باقی مانده باشد، خصوصاً مسئلهای
که معلوم شود برای حوزههایی اهمیت حیاتی دارد که در زمان مطرح شدن مسئله اصلاً
وجود نداشت. در میان این افراد کمنظیر، شاید معروفترین نمونه پییر فرما (Pierre Fermat)
باشد، که وقتی بعداً عهدهدار یک سمت رسمی دولتی شد لقب ’دو‘ به نامش اضافه
شد. ولی فرما دقیقاً یک ریاضیدان نبود. او حقوقدانی بود که در شهر تولوز مشاور
حقوقی پارلمان بود. از سوی دیگر، این کسرِ منزلت او خواهد بو که وی را یک ریاضیدان
آماتور بنامیم. شاید بتوان گفت که فرما یک ریاضیدان حرفهای بود که کارِ روزانهاش
حقوق بود.
وظایف غیر-ریاضی او وقتی را برایش باقی نمیگذاشتند تا کشفیات خودش را بنویسد،
و شاید به همین دلیل باشد که آثار چاپ شده فرما بسیار اندک است. آنچه ما از این
اکتشافات میدانیم عمدتاً بر پایه مکاتباتی است که او با ریاضیدانان و فیلسوفان هم
عصر خودش، مثل پییر دو کارکاوی (Pierre de
Carcavi)، رنه دکارت ، مارتین مرسن (Marin Mersenne)، و
بلز
پاسکال (Blaise Pascal) داشته. فرما از مفهوم اثبات ریاضی بخوبی آگاه بوده، و به ویژه تنها
عبارت نادرستی که در نوشتههای او باقیمانده (و درباره فرمولی است که او تصور میکرد
همیشه یک عدد اول را میدهد) با ادعایی همراه است که او میگوید اثباتی برای آن
ندارد. اثباتهای اندکی از او بجا مانده، که مهمترین آنها اثبات این مورد است که
جمع دو مربع نمیتواند یک عدد به توان چهار باشد، که به همراه روش بدیعی ارائه میشود
که ’نزول نامتناهی‘ (infinite
descent) نام دارد.
از جنبههای بسیار زیاد، فرما مُحق است که مشهور باشد. او پیشرفتهای عمدهای
را در هندسه حاصل کرد، در بوجود آمدن حسابان پیشگام بود، و بر روی احتملات و
فیزیکِ ریاضیِ نور کار کرد. البته مهمترین کارهایی که او در ریاضیات انجام داد به
نظریه اعداد مربوط هستند. او در این زمینه حدسی را مطرح کرد که به آخرین قضیه
فرما (Last Theorem) معروف است و برای چند صد سال شهرت او را تضمین کرد. این عبارت
ساده ولی معماگونه، نه به این دلیل آخرین نامیده میشود که او آن را در
بستر مرگش به زبان آورده، و به عبارتی آخرین کلامش بوده، بلکه به این دلیل آخرین
نامیده میشود زیرا بعدها در طول سه قرن درستی کلیه قضیههایی که او در طول حیاتش
مطرح کرده بود اثبات شدند، به غیر از این قضیه. این آخرین سنگری بود که برای فتح
آن میبایست درخشانترین اذهان بشر به آن هجوم برند.
یکی از آنها گاوس (Gauss) بود، که از بزرگترین
ریاضیدانان تاریخ محسوب میشود. تقریباً دویست سال پس از اینکه فرما این قضیه در حاشیه
کتابش را بنویسد، گاوس آن را رد کرد، و اعلام کرد این قضیه جزء آن دسته از بیشمار
عباراتی که میتوان آنها را در مورد اعداد گفت، عباراتی که نه میشود درستی، و نه
نادرستی آنها، را اثبات کرد. معمولاً معروف است که گاوس درباره مسائل ریاضی شَم
خیلی خوبی داشت، ولی این حرف او که بنظر میرسد حاکی از بیاهمیت انگاشتن آخرین
قضیه فرما است، یکی از موارد نادری بود که بعداً مشخص شد اهمیت زیادی دارد. در
دفاع از گاوس باید بگوییم که بیشتر ریاضیدانان نیز در طول سیصد و پنجاه سال گذشته
چنین حسی داشتند. تنها زمانی اهمیت این قضیه معلوم شد که شاخههای جدیدی از
ریاضیات سربرآوردند و ارتباطی که میان آنها و قضیه فرما وجود داشت معلوم گشت.
![]()
فرما در
شهر بیمان دو لومان (Beaumont-de-Lomagne) که در جنوب فرانسه واقع
است بدنیا آمد. این شهر در سال 1277 میلادی بعنوان یک دژ نظامی بنا شد، و سابقه
پرتلاطمی داشت. این شهر در طول جنگهای صدساله توسط انگلیسیها تصرف شد و 500 نفر
از ساکنان آن بر اثر طاعون جان خود را از دست دادند. آنجا یک شهر کاتولیکنشین بود
که توسط شهرهای همسایه خود، که همه پروتستان بودند، احاطه شده بود. هنری سوم
پادشاه فرانسه آن را به انگلیسیها فروخت. در اوایل سالهای 1600 پادشاه وقت
فرانسه لویی سیزدهم آن را محاصره کرد؛ در آن شهر شورشی بپا شد و در سال 1651 تحت
اشغال نظامی در آمد و تلفات زیادی داد؛ بعد از آن هم دوباره دچار طاعون شد.
پایان این سلسه رخدادها، درست مقارن شد با تولد مشهورترین ساکن این ناحیه،
یعنی پییر دو فرما. پدر پییر دومنیک (Dominique) و مادرش کلر
(Claire) نام داشتند. دامنیک یک تاجر ثروتمند بود و مادرش در خانوادهای بزرگ
شده بود که همگی در کار حقوق بودند. تردیدهایی درباره تاریخ تولد پییر وجود دارد،
بعضی آنرا 1601 و بعضی هم آن را 1607 ذکر کردهاند. دلیلش هم این میتواند باشد که
او یک برادر بزرگتر داشته، که نام او هم پییر بوده و در کودکی مرده. پدر او نیز
مانند خودش مشاور پارلمان بیمان-دو-لومان بود، بنابراین او در یک خانواده اهل
سیاست بزرگ شد. منسبی که پدرش داشت دال بر این است که او در شهر زادگاهش بزرگ شده
بود، و اگر چنین باشد، او باید در صومعه فرانسیسکانها درس خوانده باشد.
بعد از سپری کردن دورهای در دانشگاه تولوز، او به باردو رفت، و در آنجا
بود که استعداد ریاضی او شکفته شد. اولین کار او اصلاح یکی از آثار گم شده هندسهدان
یونانی آپولونیوس بود. سپس به موضوعاتی مثل حداقل و حداکثر پرداخت، که جزء
نخستین کارهایی است که در باب حسابان انجام میگرفت.
هنگامی که او از دانشگاه اورلئان مدرک حقوق خودش را دریافت کرد، کار حقوقی او
نیز شکوفا شد. در سال 1631 او در پارلمان تولوز منسبی بعنوان مشاور بدست آورد، و
از آن زمان لقب ’لو‘ به نام او اضافه شد. او بقیه عمرش را به همین کار
اشتغال داشت. او ابتدا در پارلمان سُفلی بکار مشغول بود، ولی در سال 1638 به
پارلمان عُلیا رفت، و در سال 1652 به سمت رئیس دادگاه جنایی برگزیده شد. ارتقاء
مقام فرما متوقف نشد و باز هم ادامه یافت، بخشی از دلیل آن هم این بود که طاعون در
دهه 1650 بسیاری از مقامات عالیرتبه را هلاک کرده بود و باید برای آنها جانشینانی
پیدا میشد. در سال 1653 شایعه اغراقآمیزی رواج پیدا کرد که حتی فرما هم در اثر
طاعون هلاک شده. ولی بعداً معلوم شد که فرما وظایف حقوقی خودش را تعطیل کرده و از
فرصت استفاده کرده و به علایق ریاضی خودش پرداخته.
در سال 1629 او کتاب ’مقدمهای بر مکانهای هندسی مسطح و فضایی‘ را
نوشت که پیشگام استفاده از دستگاه مختصات در هندسه و جبر بود. غالباً اعتبار این
ایده را به دکارت نسبت میدهند که در 1637 آن را در کتاب هندسه خودش
مطرح کرده بود. در این روش از یک جفت محور مختصات استفاده میشود، و برای نمایش هر
نقطه از یک جفت عدد بصورت (x,y)
استفاده میشود، روشی که امروزه چنان پیش و پا افتاده است که به ندرت نیاز به
توضیح دارد.
در کتابش بنام ’در باب مماس بر منحنیها‘ که در سال 1679 نوشت، چگونگی
یافتن مماس بر منحنیها را کشف میکند، که نسخه هندسی حساب دیفرانسیل است. از موارد دیگری که
او را به یکی از پیشگامان حسابان بدل میسازد، روشی است که او برای پیدا کردن بیشینه (maxima) و کمینه (minima)
پیدا کرد. در نورشناسی او اصل کمترین زمان را مطرح کرد، که میگوید یک پرتو
نور مسیری را طی میکند که کل زمان حرکت به حداقل برسد. این یکی از اولین قدمها
در راه مبحثِ حساب تغییرات (calculus
of variations) بود، که یکی از شاخههای
آنالیز است و یک منحنی یا سطحی را جستجو میکند که یک کمیت مرتبط را کمینه یا
بیشینه کند. برای مثال، کدام سطح بسته است که دارای حجم ثابت ولی کمترین مساحت
است؟ جواب دایره است، و این توضیح میدهد که چرا
حبابهای صابون به شکل کروی هستند، زیرا انرژی کشش سطحی متناسب با سطح است، و حباب
شکلی را به خودش میگیرد که انرژی را به حداقل برساند.
به طریق مشابهی، او با دکارت بر سر قانون شکست نو بحث میکند. دکارت که
احتمالا بخاطر گرفتن اعتبار دستگاه مختصات از سوی فرما نارحت بود، و خودش را مستحق
این اعتبار میدانست، با حمله بر روشهای فرما برای یافتن ماکزیمم و مینیمم، و
یافتن مماس به او پاسخ داد. این بحثها چنان بالا گرفت که مهندس و هندسهدان مطرح
فرانسوی، ژِرارد دزارگ (Girard
Desargues)، مجبور شد میان آنها نقش
داور را بازی کند. هنگامی که او گفت حق با فرما است، دکارت بااکراه این را پذیرفت
و گفت: ”اگر شما از ابتدا این را به این صورت مطرح کرده بودید، من هیچ مخالفتی با
آن نداشتم.“
![]()
بزرگترین دستآوردهای فرما به نظریه اعداد مربوط هستند. نامههایی که او به
ریاضیدانان دیگر نوشته حاوی چالشهای فراوانی در این حوزه است. از میان آنها میتوان
به این مورد اشاره کرد که ’مجموع دو مکعب کامل نمیتواند مکعب کامل باشد‘، و
همچنین معادلهای که به اشتباه به معادله پِل معروف است و به شکل nx2 + 1 = y2 بیان میشود. در اینجا n یک عدد صحیح مفروض، و x و y
اعداد مجهول معادله هستند که باید یافت شوند. لئونارد اویلر به اشتباه یکی از راهحلهای
این معادله را به جان پِل (John
Pell) نسبت میدهد. در واقع براهماگوپتا
در سال 628 روشی برای حل این معادله ارائه داد.
یکی از مهمترین و زیباترین نتایجی که فرما حاصل کرد مربوط به اعدادی است که میتوانند
بصورت مجموع دو مربع کامل بیان شوند. در سال 1634 برای اولین بار آلبرت ژیرار (Albert Girard)
جواب آن را در یکی از کتابهایش مطرح کرد. ولی فرما اولین کسی بود که در سال 1640
طی نامهای که به مرسن نوشت ادعا کرد که اثباتی برای آن دارد. نکته اصلی این اثبات
در آن بود که مسئله باید برای اعداد اول حل شود. جواب به نوع عدد اول بستگی دارد.
تنها عدد اول زوج 2 است. اعداد فرد یا مضربی از 4 بعلاوه 1
هستند یا مضربی از 4 بعلاوه 3؛ یعنی آنها را میتوان بصورت 4k+1 یا 4k+3 نوشت. همین برای بقیه اعداد اول نیز صادق است (زیرا بقیه اعداد
اول همه فرد هستند). فرما ثابت کرد که 2، و هر عدد اولی که بصورت 4k+1 باشد، مجموع دو مربع هستند؛ از سوی دیگر، آنهایی که بصورت 4k+3 باشند اینطور نیستند.
اگر خودتان آزمایش کنید، درک این موضوع آسان خواهد بود. برای مثال 13=4+9=22+32، و 13=4×3+1. از سوی دیگر 7=4×1+3، و مجموع دو
مربع نمیتواند مساوی 7 باشد. آسانترین کار این است که نشان دهیم
اعداد اولی که به شکل 4k+3 هستند مجموع دو مربع نیستند. من بعداً در فصل 10 با استفاده از روشی که گاوس در نظریه اعداد ابداع کرد،
چگونگی اینکار را به شما نشان میدهم. ولی بخش دیگر اثبات این قضیه این است که
نشان دهیم اعداد اولی که به شکل 4k+1 هستند،
مجموع دو مربع میباشند، و این کار بسیار دشوارتری محسوب میشود. اثباتی که
فرما برای این ارائه داد، در دست نیست، ولی گمان بر این است که او از روشهایی
استفاده کرده بود که برای او قابل دسترس بودند. اولین اثبات قطعی برای این قضیه
توسط اویلر کشف شد، که خبر آن را در سال 1747 اعلام، و طی دو مقاله در سالهای
1752 و 1755 آنها را منتشر کرد.
خلاصه کلام این است که یک عدد صحیح وقتی مجموع دو مربع است که اگر عدد تجزیه
شود، همه عواملِ اول آن که به شکل 4k+3 هستند، در یک توان زوج ظاهر شوند. برای مثال 245=5×72 . در اینجا عامل 7 بصورت 4k+3
است، و در یک توان زوج ظاهر شده، بنابراین میتوان مطمئن بود که 245
مجموع دو مربع کامل است. در واقع 245=142+72. در
مقابل عددی مثل 35 برابر است با 5×7، و در اینجا 7
بصورت یک توان فرد ظاهر شده (1)، بنابراین مطمئناً 35
مجموع دو مربع صحیح نیست. بنظر میرسد این نتایج فقط حاصل کنجکاوی محض باشند، ولی
این مسئله منشاء تحقیقات زیادی در نظریه اعداد بود، چیزی که نهایتاً به نظریه
فراگیر فرمهای درجه دوم (quadratic
forms) گاوس انجامید (به فصل 10 رجوع کنید). بعدها این مسئله بسط خیلی بیشتری یافت. مثلاً
قضیه مشابهای هست که توسط لاگرانژ (Lagrange) اثبات شد و
میگوید هر عدد صحیح مجموع چهار مربع است (البته بشرطی که 0=02 قابل قبول باشد). این مسئله نیز تاثیرات گستردهای بر نظریه اعداد گذاشت.
![]()
داستان آخرین قضیه فرما بارها از زبان تاریخدانان و ریاضیدانان مختلف گفته
شده، ولی من به هیچوجه متاسف نیستم که دوباره آن را بازگو کنم، زیرا داستان مهمی
است.
شاید طعنهآمیز باشد که بیشترین شهرت فرما بواسطه قضیهای است که مطمئناً هیچ
اثباتی برای آن ارائه نداد. ظاهراً او ادعا کرده بود که اثباتی برای
این قضیه دارد، و حالا معلوم شده که این ادعا درست بوده، ولی قضاوت تاریخ این است
که روشهایی که در آن زمان در اختیار او بوده، اجازه اثباتِ چنین قضیهای را نمیدادهاند.
او ادعا کرده بود که اثباتی در اختیار دارد ولی چون حاشیه کتابش اجازه نوشتن آن را
نمیدهد، آن را در جای دیگری خواهد نوشت، چیزی که هیچ وقت پیدا نشد، بنابراین آن
اثبات فقط میتواند چیز ناپخته و ناقصی بوده باشد. در دنیای ریاضیدانان این چیز
غیر عادی نیست که شما صبح از خواب بیدار شوید و به این نتیجه برسید که چیز مهمی را
اثبات کردهاید، ولی وقتی آن را در معرض دید بقیه گذاشتید، نتیجهگیری شما تا ظهر
هم پابرجا نخواهد بود و معلوم میشود یک جای کار اشتباه بوده.
کتابی که فرما مشغول مطالعه آن بود ترجمه فرانسوی کتاب حساب دیافانتوس (Diophantus)
بود، که البته اگر کتاب اصول اقلیدس را کنار بگذاریم، میشود آن را اولین
اثر در نظریه اعداد بحساب آورد. مطمئناً کتاب دیافانتوس اولین متن تخصصی در این
زمینه است. بخاطر داشته باشید که در ریاضیات نام معادلات دیوفانتی
(Diophantine equation)، که به
معادلات سیاله نیز معروف هستند، برگرفته
از نام همین ریاضیدان است. اینها معادلاتی چندجملهای هستند که باید برای آنها
جوابهای صحیح یا گویا پیدا شود. دیافانتوس برای چنین
معادلاتی یک کاتالوگ نظاممند ساخت. یکی از گونههای این معادلات بصورت x2 + y2 = z2 است، که سهگانههای فیثاغورثی
نامیده میشوند، دلیل آن هم این است که در یک مثلث قائمالزاویه که اضلاع آن x، y، و z
باشند، معادله از قضیه فیثاغورث پیروی میکند و دقیقاً به شکل بالا بیان میشود.
سادهترین حل این معادله اعداد 3، 4، و 5
هستند. این معادله دارای بینهایت جواب است که اقلیدس رویهای برای تولید همه آنها
پیدا کرد، و دیافانتوس نیز آن را در کتابش گنجانده بود.
فرما یک نسخه از ترجمه فرانسوی این کتاب را در اختیار داشت و هر از چندگاهی در
حاشیه این کتاب مطالبی را یادداشت میکرد. بر طبق گفته پسر فرما، ساموئل،
آخرین قضیه در یادداشتی آمده که به مسئله هشتم فصل دوم کتاب الصاق شده بود. ما این
را از این جهت میدانیم که ساموئل بعداً نسخهای از کتاب حساب دیافانتوس را منتشر
کرد که در آن یادداشتهای پدرش نیز آمده بود. تاریخ این یادداشتها مشخص نیستند،
ولی فرما خواندن کتاب دیافانتوس را در حولی سال 1630 شروع کرده بود. فرض بر
این است که فرما در زمانی که میخواسته قضیه فیثاغورث را تمیم دهد، محسور این
مسئله شده، و همین به یادداشت حماسی او منجر شد:
”این غیر ممکن است که بتوان یک توان سوم را بصورت مجموع دو توان سوم، یا یک
توان چهارم را بصورت مجموع دو توان چهارم، یا هر توان دیگری که از دو بزرگتر باشد
را بصورت مجموع دو توان مشابه بیان کرد. حقیقتا من اثبات شگفتانگیزی را برای این
قضیه کشف کردهام، ولی حاشیه این کتاب اجازه نوشتن آن را نمیدهد.“
این یعنی اگر n
بزرگتر از دو باشد، معادله دیوفانتی xn + yn
= zn دارای هیچ جواب صحیحی نیست.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

آیزِک نیوتون[2] (Isaac Newton): تولد: 4 ژانویه 1643 میلادی، انگلستان. وفات: 31 مارس 1727 میلادی.
در سال
1696 ضرابخانه سلطنتی، که مسئول تولید پول برای انگلستان بود، سرپرست جدیدی پیدا
کرد. نام این شخص آیزِک نیوتون بود. این منصب توسط چارلز مونتاگ،
که در آن زمان وزیر خزانهداری بود، به او داده شد. نیوتون مسئول ضرب سکههای
مملکت شد. در آن زمان مسکوکات بریتانیا در وضعیت بدی قرار داشت. نیوتون برآورد
کرده بود که تقریباً 20 درصد سکههای درگردش یا جعلی بودند، یا آنها را بریده
بودند، یعنی سکههای طلا یا نقره را از لبههای آنها تراش داده بودند، تا
باقیمانده آنها را ذوب کرده و در بازار بفروشند. اساساً جعل سکه یا تراش آن خیانت
محسوب میشد، و مجازات آن هم مرگ همراه با شکنجه بود. ولی در عمل هیچکس به
این جرم متهم نشد، چه رسد که بخاطر آن مجازات شود.
بعنوان کسی که در سابقه کاری خودش سمت استاد ریاضیات دانشگاه کمبریج را داشت،
این سرپرست جدید با بقیه فرق میکرد. او کسی بود که خلق و خوی عجیبی داشت، و تمام
عمرش را با موضوعات دشواری مثل ریاضیات، فیزیک، و کیمیاگری سپری کرده بود. او
همچنین رسالههای مذهبی برای تفسیر انجیل نوشته بود، و تاریخ آفرینش را 4000 ق.م
تعیین کرده بود. او در سالهای 1689 تا 1690 از طرف دانشگاه کمبریج بعنوان عضو
پارلمان خدمت کرده بود، و اینکار را از سال 1701 تا 1702 تکرار کرد، ولی گفته میشود
تنها سخنی که او یکبار در آنجا بیان کرده بود این بوده که هوای تالار سرد است و او
خواسته تا پنجرهها را ببندند! به آسانی میتوان فرض کرد که سمتهای دولتی که او
کسب کرده از طریق حامیان سیاسی بوده، و کلاً از این نظر فرد مطیعی بحساب میآمده.
یک سال پس از کسب سمت سرپرست ضرابخانه توسط نیوتون، 28 تن از کسانی که این
جرم را مرتکب شده بودند فهمیدند که اینبار با گذشته تفاوت دارد. نیوتون تحقیقات
خودش را از طریق روشهایی انجام میداد که بیشباهت به کارهای شرلوک هولمز
نبود. او بطور ناشناس خودش را به شکل مشتریان بدنام میخانهها و آبجوفروشیها درمیآورد
و جاسوسی مشتریانی را میکرد که به آنجا میآیند، و منتظر میشد تا عمل مجرمانهای
صورت گیرد. نیوتون فهمیده بود بزرگترین مانع در پیگرد موفق مجرمین، طبیعتِ مبهم
قوانین انگلیس بود، به همین جهت به روشهای و سنتهای قدیمی متوسل شد. در آن زمان
در دستگاه قضایی انگلستان سمتی وجود داشت که به امینالصلح معروف بود و اختیارات
قضایی فراوانی داشت. او میتوانست مجرمین را تحت پیگرد قرار دهد، از شهود بازجویی
کند، و تا اندازه زیادی هم بعنوان قاضی و هم بعنوان هیات منصفه عمل کند. بنابرای
کاری که نیوتون کرد این بود که در تمام شهرهای نزدیک لندن بعنوان امینالصلح منسوب
شود. در طول هجده ماه، که از تابستان 1698 شروع شد، او بیش از صد شاهد، مظنون، و
خبرچین را مورد بازجویی قرار داد و همانطور که اشاره شد، از میان آنها 28 نفر را
محکوم کرد.
ما بطور اتفاقی از این فعالیتهای نیوتون اطلاع داریم، دلیلش هم این است که
نیوتون در این باره نامهای نوشته بود و آن را لای نسخه کتاب اصول خودش (Principia)
گذاشته بود. کتاب اصول، مهمترین اثر نیوتون است که در آن قوانین فیزیک و ریاضی
حاکم بر حرکت و گرانش را توضیح میدهد، و در آن طیف وسیعی از پدیدههای طبیعی را
شرح میدهد.
داستان فوق گویای این است که هر موقع نیوتون تمرکز خودش را بر روی چیزی میگذاشته،
معمولاً به نتایج قابل توجهی دست پیدا میکرده، هر چند در کیمیاگری، و در تحقیقات
دینی اینطور نبود. از مناصب دیگر او میتوان به رئیس انجمن سلطنتی، و دریافت نشان
شوالیه از طرف ملکه در سال 1705 اشاره کرد. ولی بزرگترین خدمتی که او به جامعه
بشری کرد در زمینه ریاضیات و فیزیک بود. او حسابان (calculus) را اختراع
کرد و از آن برای شرح قوانین اساسی جهان استفاده کرد، و همان چیزی است که او در
عنوان فرعی کتاب اصول خودش از آن بعنوان نظام گیتی (System of the World)
یاد میکند.
ولی شروع کار او بسیار فروتنانه بود.
![]()
نیوتون در روز کریسمس سال 1642 بدنیا آمد. حداقل این تاریخی است که بعنوان
زادروز او ثبت شده. ولی این تاریخ بر اساس تقویم ژولی (Julian calendar)
بود، که بدلیل داشتن ’روزهای گمشده‘ بدنام بود. این تقویم بعدها با تقویم
گریگوری (Gregorian calendar) جایگزین شد، و با این حساب تاریخ تولد نیوتون 4 ژانویه 1643
خواهد بود. او بچگی خودش را در مزرعهای در وولزثروپ (Woolsthorpe)
سپری کرد، که جزیی از شهرستان لینکلنشایر است.
پدر نیوتون، که نام او هم آیزِک بود، دو ماه پیش از تولد پسرش فوت کرد.
خانواده نیوتون مزرعهدار بودند، و پدرش صاحب یک مزرعه بزرگ، یک خانه، و احشام
فراوان بود. مادر نیوتون، که هانا نام داشت، مزرعه را اداره میکرد. هنگامی
که آیزک دو ساله بود، هانا با کشیش دهکده ازدواج کرد. آیزِک کوچک در وولزثروپ تحت
مراقبت مادربزرگش بود. دوران کودکی او با خوشحالی همراه نبود، و میانه او با
پدربزرگش چندان خوب نبود، حتی از این بدتر میانه او با مادر و ناپدریش نیز خوب
نبود. هنگامی که او در سن 19 سالگی در کلیسا به گناهان خودش اقراق میکند، چیزی که
از آن طلب بخشش میکند این بوده که تهدید کرده خانه مادر و ناپدریش را آتش بزند تا
آنها در آن بسوزند.
ناپدری او در سال 1653 فوت کرد، و آیزک به مدرسه فری گرامر در گرانتام
رفت، جایی که با خانواده کلارک همخانه شد. ویلیام کلارک یک داروساز بود که خانهاش
در بالای خیابان و در جنب مسافرخانه جورج قرار داشت. نیوتون در میان ساکنان
شهر بخاطر اختراعات عجیب و دستگاههای مکانیکی که داشت معروف بود. او بجایی اینکه
با بچهها بازی کند، پول تو جیبی خودش را صرف خرید ابزارآلات میکرد، و با آنها
خانههای چوبی کوچک، یا آسیاب بادی میساخت. او یک یک پله گَردان (تردمیل)
ساخت که یک موش میتوانست روی آن بدود و یک چرخ کوچک را به حرکت درآورد. او یک
فانوس کاغذی درست کرد که به یک بادبادک متصل میشد و هنگام شب همسایهها را وحشتزده
میکرد. زندگینامهنویس او ویلیام استُکِلی دراینباره میگوید: ”این اختراع
او برای مدتی همه همسایگان و ساکنان شهر را وحشتزده کرد، و مردم روزها درباره آن
حرف میزدند.“
از آن موقع به بعد، تاریخنگاران منبع بیشتر اختراعات نیوتون را پیدا کردند، و
آن کتاب رازهای طبیعت و هنر نوشته جان بِیت بود. یکی از دفترهای
نیوتون حاوی تِکههای فراوانی از این کتاب است. هرچند این اختراعات دست اول نبودهاند،
ولی نشان میدهند که تمرکز اولیه او بر روی موضوعات علمی بوده. او به ساعتهای
آفتابی علاقه زیادی داشت (در کلیسای کلسترورث نیز یکی از این ساعتها قرار
دارد که ساخت آن را به نیوتون نسبت میدهند)، و آیزک جوان در خانه کلارک آزادانه
از این ساعتها میساخت. او بر روی دیوارهای خانه میخهای چوبی کوفته بود که
نشاندهنده ساعات، نیمساعات، و ربعساعات بود. او یادگرفت که چگونه با دقت کافی
تاریخ وقایع مهم نجومی، مثل انقلابین یا اعتدالین را تعین کند، طوری که خویشاوندان
و همسایهها به آنجا میآمدند تا ’ساعت آیزک‘ را ببینند. او میتوانست با مشاهده
سایههایی که در اطاق هستند بگوید ساعت چند است. او که پیش یک داروساز زندگی میکرد
از این فرصت استفاده کرد تا با ترکیب داروها آشنا شود، که این مقدمهای بر شیمی
بود و باعث شد او بعداً به کیمیاگری علاقهمند شود. او با ذغال نقاشیهای خوبی از
پرندگان، حیوانات، کشتیها، و حتی تصویر آدمها را بر روی دیوارهای اتاقش میکشید.
معلوم بود که او جوان بااستعدادی است، ولی هیچ نشانه خاصی از اینکه به
ریاضیات علاقه دارد از خودش نشان نداد، و کارنامه مدرسه از او بعنوان یک دانشآموز
تنبل و بیتفاوت یاد میکند. در آن زمان رسم بود که امور مالی خانواده را پسران
ارشد در دست میگرفتند، و به همین دلیل مادرش آیزک را از مدرسه بیرون آورد تا
حسابداری بیآموزد و در کار مدیریت املاک به او کمک کند. ولی او حتی نسبت به این
کار علاقه کمتری از خودش بروز داد. یکی از داییهایش مادرش را متقاعد کرد که او را
به دانشگاه کمبریج بفرستد، بنابراین او دوباره آیزک را به گرانتام فرستاد تا
تحصیلات پیشدانشگاهی خودش را تکمیل کند.
او در سال 1661 به کالج ترینیتی، که بخشی از دانشگاه کمبریج بود، وارد
شد، و میخواست حقوق بخواند. درسها بر اساس فلسفه ارسطویی بود، ولی در سال سوم
دانشجوها میتوانستند آثار ریاضیدانِ فیلسوف دکارت، فیلسوفِ دانشمند پییر گاسندی (Pierre Gassendi)، توماس هابز دانشمند، و رابرت بویل فیزیکدان را بخوانند.
نیوتون آثار گالیله را مطالعه کرد، مطالبی را درباره نجوم و نظریه کپرنیک که میگفت
زمین بدور خورشید میگردد یادگرفت. کتاب نورشناسی کپلر را خواند. اینکه
چگونه نیوتون با ریاضیات پیشرفته آشنا شد زیاد معلوم نیست. آبراهام دو موآ (Abraham de Moivre) مینویسد
که آشنایی نیوتون با ریاضیات از هنگامی آغاز شد که او یک کتاب طالعبینی خرید و
نمیتوانست ریاضیات آن را بفهمد. او که میخواست در مثلثات تسلط پیدا کند، فهمید
که به اندازه کافی هندسه نمیداند، بنابراین کتاب اصول اقلیدس ترجمه آیزِک
بارو (Isaac Barrow) را مطالعه کرد. این کتاب برای او ساده بنظر میآمد، تا اینکه به
قضیهای درباره مساحت متوازیالاضلاعها رسید، و او را تحت تاثیر قرار داد. سپس او
بسرعت شروع به مطالعه آثار مهم ریاضی نمود، کتابهایی مثل کلید ریاضیات اثر ویلیام اوترد (Oughtred)،
هندسه دکارت، آثار فرانسوا ویته (François Viète)، و جبر
نوشته جان والیس (John
Wallis). والیس از اینفینیتسیمالها، یا بینهایت کوچکها (infinitesimals)
برای محاسبه مساحت زیر یک سهمی و هذلولی استفاده کرد. نیوتون، که درباره این روش
فکر کرده بود اینطور نوشت ”هرچند والیس اینکار را کرد، ولی آن را میتوان به این
صورت هم انجام داد ...“ او قبلاً خودش به چنین ایدهها و اثباتهایی رسیده بود،
ایدههایی که از ریاضیدانان بزرگ الهام گرفته بود، ولی خیلی از آنها تعریف نمیکرد.
روشهای والیس جالب بود، ولی به هیج وجه منحصر به فرد نبودند. نیوتون میتوانست بهتر
عمل کند.
در سال 1663 بارو صاحب کرسی لوکاسین شد، و به عضویت هیئت علمی
کالج ترینیتی، یعنی همانجایی که نیوتون در آنجا دانشجو بود، درآمد. ولی هیچ نشانهای
وجود ندارد که او متوجه استعداد خاصی در این دانشجوی جوان شده باشد. استعداد او
هنگامی شکوفا شد که در سال 1665 بخاطر شیوع طاعون بزرگ، دانشجویان به خانههای
خودشان فرستاده شده بودند. در سکوت و آرامش ییلاقات لینکلنشایر، که به دور از
غوغای شهر بود، نیوتون توجه خودش را به علم و ریاضیات معطوف کرد. میان سالهای 1665
و 1666 او بر روی قانون جاذبه کار کرد، قانونی که میتوانست حرکت ماه و
سیارات را توضیح دهد، و نیز قوانین مکانیک را ابداع کرد که حرکت اجسام متحرک را
توضیح دهد. او همچنین حساب دیفرانسیل و انتگرال را اختراع کرد، و کشفیات عمدهای
را در زمینه نورشناسی انجام داد. او هیچ یک از کارهایش را منتشر نکرد، ولی به
کمبریج بازگشت تا مدرک کارشناسیارشد خودش را بگیرد، و در آن زمان بعنوان عضو هیئت
علمی کالج ترینیتی برگزیده شد. هنگامی که بارو در سال 1669 بازنشسته شد، نیوتون
بجای او بعنوان استاد لوکاسین ریاضیات منسوب شد، و در سال 1672 به عضویت انجمن
سلطنتی درآمد.
نیوتون از سال 1690 به بعد رسالههای متعددی درباره تفسیر انجیل نوشت و به
آزمایشات کیمیاگری پرداخت. او به پستهای مدیریتی فراوانی دست پیدا کرد، و سرانجام
سرپرست ضرابخانه سلطنتی شد. او در سال 1703 بعنوان رئیس انجمن سلطنتی انتخاب شد، و
هنگامی که ملکه آن (Anne) در سال 1705 از کالج ترینیتی دیدار کرد، به او نشانه شواله داد.
تنها دانشمندی که پیش از نیوتون توانسته بود این نشان را دریافت کند فرانسیس بِیکن (Francis Bacon)
بود. با ورشکستگی شرکت ساوت سی (South Sea)، نیوتون
نیز قسمت عظم سرمایه خودش را از دست داد، و مجبور شد به وینچستر برود و با
خواهرزاده خودش زندگی کند، و تا هنگامی که در سال 1727 در خواب فوت کرد، در همانجا
بود. ظن پزشکان به مسمومیت با جیوه بود، زیرا در میان موهای او اثرات جیوه پیدا
شده بود. با توجه به آزمایشات کیمیاگری که او انجام میداد، چنین چیزی دور از
انتظار نبود، و میتوانست رفتار غیرعادی او را در زمان پیری توضیح دهد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

لئونارد اویلر (Leonhard Euler): تولد: 15 آوریل 1707
میلادی، بازل سوئیس. وفات: 18 سپتامبر 1783 سنپیترزبورگ روسیه.
شاید
در دوران ما لئونارد اویلر مهمترین ریاضیدانی باشد
که نام او برای عموم مردم ناشناخته است. ولی در دوران حیاتش او چنان اعتباری داشت
که وقتی ارتش روسیه در سال 1760 مزرعه او را در جنگِ هفت ساله ویران کردند،
فرمانده کل سپاه ژنرال ایوان سالتیکو فوراً دستور داد تا خسارت او جبران
شود. الیزابت، امپراتريس روسیه، دستور داد که 4000 روبل دیگر نیز به این پول اضافه
شود، که در آن زمان مبلغ قابل ملاحظهای بود. ولی این پایان ماجرا نبود. اویلر که
از سال 1726 عضو آکادامی سنتپیترزبورگ بود، در سال 1741 با وخیم شدن اوضاع سیاسی
روسیه، آنجا را به مقصد برلین ترک کرد. در سال 1766 به روسیه بازگشت، و درخواست
حقوق سالیانهای معادل 3000 روبل، یک حقوق بازنشستگی سخاوتمندانه برای همسرش، و
اینکه به پسرانش مناصب پرمنفعتی داده شود، را کرد.
ولی زندگی به هیچوجه برای او رضایتبخش نبود. اویلر پس از اینکه در سال 1738
بینایی چشم راستش را از دست داد، نمیتوانست درست ببیند. سپس چشم چپ او هم دچار آب
مروارید شد، و تقریباً بطور کامل کور شد. ولی او دارای حافظه شگفتانگیزی بود؛ او
میتوانست کل یک کتاب شعر را از بر بخواند، اگر به او شماره صفحه یک کتاب را میدادید،
میتوانست خط اول و خط آخر آن صفحه را به شما بگوید. یکبار که بیخوابی به سرش زده
بود، و گوسفند شمردن نیز بنظرش مسخره میآمد، تصمیم گرفت توان ششم کلیه اعداد را
تا 100 حساب کند. چندین روز بعد، او هنوز میتوانست نتیجه محاسباتی که کرده بود را
بخاطر بیاورد. پسران اویلر، که یوهان و کریستوفر نام داشتند، اغلب
به همراه دو تن از اعضای آکادامی بعنوان منشی او عمل میکردند. نوه اویلر، نیکولای
فاس، نیز از سال 1776 بعنوان دستیار رسمی او شروع بکار کرد. کلیه این افراد بخوبی
ریاضیات میدانستند و اویلر ایدههای خودش را با آنها درمیان میگذاشت. این همکاری
چنان موفق بود که حتی پس از اینکه او بینایی خودش را هم از دست داد، دستآوردهای
شگفتانگیزش از قبل هم زیادتر شد.
تقریباً هیچ چیز نمیتوانست مانعی برای کار کردن اویلر باشد. در سال 1740 او
در آکادمی برلین تعداد زیادی از پستهای مدیریتی را عهدهدار شد، چیزهایی مثل
سرپرست باغ گیاهشناسی و رسدخانه، مسئول استخدام، مدیر مالی، سرپرست انتشار نقشهها
و تقویمها، ... . او برای ترمیم کانال فینلو و سیستم آبیاری بعنوان مشاور
شاه فردریک عمل میکرد. شاه از این کار راضی نبود و گفته بود: ”من میخواستم
در باغم یک فواره داشته باشم. اویلر نیروی لازم برای چرخهای بالا برنده آب به
منبع را حساب کرد. ولی این آسیابی که با محاسبات هندسی ساخته شده حتی نمیتواند
مقدار کمی آب را به ارتفاع پنجاه قدمی منبع ببرد. این هندسه همهاش بیهود است!
بیهوده!“
مدارک تاریخی نشان میدهند که فردریک اشتباه میکرد و شخص اشتباهی را مقصر میدانست.
معماری که باغ فردریک را ساخت، مینویسد که او تعداد زیادی فواره میخواسته، که
بزرگترین آنها باید آب را به ارتفاع 30 متری پرتاب میکرده. تنها منبع برای تامین
آب، رودخانه هاول بود، که 1500 متر با آنجا فاصله داشت. نقشه اویلر این بود
که از رودخانه یک کانال بزرگ حفر کند تا به یک پمپ برسد که با آسیاب بادی چرخانده
میشد. این میتوانست آب را به منبعی برساند که با سطح باغ در حدود 50 متر اختلاف
ارتفاع داشت و میتوانست فشار لازم برای جهش آب در فوارهها را فراهم آورد. در سال
1748 ساخت و ساز شروع شد و تا وقتی که لولههایی که از پمپ به منبع میرفتند نصب
شدند، بدون هیچ مشکلی ادامه یافت. این لولهها از چوبهای باریکی ساخته شده بودند
که دور آنها نوارهای آهنی بود، چیزی شبیه بشکه. درست هنگامی که پمپاژ آب به داخل
منبع شروع شد، این لولهها ترک برداشتند. بنابراین مجبور شدند از لولههای فلزی
استفاده کنند، ولی قطر این لولهها کوچک بود و نمیتوانستند فشار کافی برای آب
فراهم آورد. تلاش برای حل این مشکل تا سال 1756 ادامه یافتند، و در زمان جنگ هفت
ساله متوقف، و پس از وقفه کوتاهی از سر گرفته شد. در آن زمان دیگر حوصله شاه سر
رفته بود و پروژه متوقف شد. معمارِ پروژه خود شاه را سرزنش میکرد که عادت داشت
سازههای باعظمتی را سفارش دهد ولی پول کافی برای آنها فراهم نمیکرد. گزارشهای
این معمار همه را مسئول این شکست میدانست، ولی نام اویلر در میان آنها نبود.
در واقع کار اویلر در طراحی این پروژه اساس نظریه جریان هیدرولیک در لولهها،
و اینکه چگونه حرکت آب بر فشار لولهها تاثیر میگذارد، را گذاشت. بویژه او نشان
داد که حتی اگر هیچ اختلاف ارتفاعی در کار نباشد، حرکت موجب میشود تا فشار زیادتر
شود. علم هیدرولیک سنتی چنین چیزی را پیشبینی نمیکرد. اویلر افزایش فشار را
محاسبه کرد، توصیههایی در مورد پمپ و لولهها ارائه داد، و اکیداً به سازندگان
هشدار داد که کارهایی که میکنند سرهم بندی است و اگر اینطور پیش بروند، بالاخره
پروژه با شکست روبرو میشود.
او اصرار داشت تا بجای لولههای چوبی از لولههای سربی استفاده شود، و ضخامت
سرب باید از طریق آزمایش کاهش یابد. توصیههای او نادیده گرفته شد.
شاه فردریک احترام خیلی زیادی برای دانشمندان قایل نبود، و هنرمندانی مثل ولتر (Voltaire) را
ترجیح میداد. او چشم نابینای اویلر را مسخره میکرد و اسم او را ’غولِ یک
چشمِ ریاضی‘ گذاشته بود.
وقتی فردریک درباره پروژه باغ نوشت، سی سال از آن زمان گذشته بود، و اویلر سالها
بود که از آلمان به روسیه رفته بود، پس او شخص مناسبی بود تا تقصیرها بر گردن او
انداخته شود. ولی او به دولت در اموری مثل بیمه، مالیات، توپخانهها، و قرعهکشی
مشورت میداد. اگر چیزی به ریاضیات ربط داشت، او مرد همه-کاره دوران خودش بود. و
در طول این مدت، کارهای او بطور ثابت بر تحقیقات اصلی آن زمان و کتابهای درسی
نفوذ پیدا میکرد.
او تا روز مرگش هم هنوز کار میکرد. در یک روز عادی مثل همه روزها، او به یکی
از نوههایش ریاضی درس داد، درباره بالونها چند محاسبه کوچک انجام داد، و درباره
کشف سیاره تازه کشف شده اورانوس با دانشمندانی مثل لِکسل (Lexell) و فاس
(Fuss)
صحبت کرد. بعد از ظهر او دچار خونریزی مغزی شد، و گفت ’دارم میمیرم‘، و شش ساعت
بعد درگذشت. نیکولاس کوندورسه در کتابی بنام در ستایش آقای اویلر مینویسد
”در آن موقع بود که اویلر از زندگی و محاسبه باز ایستاد.“ برای اویلر ریاضیات
همانقدر عادی بود که نفسکشیدن.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

ژوزف فوریه (Joseph Fourier): تولد: 21 مارس 1768 ،
فرانسه. وفات: 16 می 1830.
سال
1804 بود و دوران فیزیکِ ریاضی آغاز شده بود. یوهان برنولی قوانین حرکت نیوتون را با
قانون هوک درباره فنرها، و نیز ارتعاشات تارهای یک ویولون، همه را با هم ترکیب
کرده بود. ایدههای او به این منجر شد که ژان دالمبر (Jean d’Alembert) معادله موج
را فرمولبندی کند. این یک معادله دیفرانسیل است که نرخ تغییراتِ شکلِ تار را هم
نسبت به زمان، و هم نسبت به فضا، به هم مرتبط میکند. رفتار همه موجها از این
معادله پیروی میکنند، از امواج آب گرفته، تا امواج صوتی، و دیگر ارتعاشات.
معادلات مشابهای نیز برای مغناطیس، الکتریسیته، و گرانش پیشنهاد شده بودند. حالا
نوبت ژُزف فوریه بود تا همین روشها را برای حوزه دیگری از فیزیک بکار
بگیرد، یعنی بررسی جریان گرما در یک محیط رسانا. بعد از سه سال تحقیق، فوریه یک
یادداشت بلندبالا درباره انتشار گرما نوشت، و آن را برای موسسه پاریس فرستاد، که
در آنجا با واکنشهای مختلفی روبرو شد، پس کمیتهای تشکیل شد تا آن را بررسی کند.
سپس گزارشی تهیه شد، که بر اساس آن معلوم بود کمیته زیاد از نتیجه راضی نیست. آنها
برای نظراتشان دو دلیل داشتند، که یکی خوب و دیگری بد بود.
ژان-بابتیسته بیو (Jean-Baptiste Biot) به اعضای
کمیته گفت که مشکلی در مشتقِ معادلهِ جریان گرما وجود دارد. فوریه اشارهای به
مقالهاش در سال 1804 نکرده بود. این دلیل بد بود، زیرا مقاله بیو اشتباه بود.
دلیل خوب این بود که یک مرحله اصلی در استدلال فوریه، یعنی تبدیل یک تابع تناوبی
به یک سری نامتناهی از سینوسها و کسینوسهای یک زاویه مفروض، با دقت کافی مطرح
نشده بود. درواقع اویلر و برنولی سالها بود که در زمینه معادله موج، درمورد چنین
ایدهای استدلال میکردند. فوریه روشن کردن استدلالش را تسریع بخشید، ولی باز هم
کمیته راضی نبود.
بااینحال، این مسئله مهمی بود و فوریه تلاش زیادی برای حل آن کرد. بنابراین
موسسه پاریس اعلام کرد که مسابقه سال 1811 درمورد جریان گرما در جامدات است. فوریه
چند نتیجه دیگر نیز به یادداشت خودش درمورد سرد شدن و تابش گرما اضافه کرد، و آن
را به کمیته تسلیم کرد. کمیته جدید جایزه آن سال را به او داد، ولی همان ملاحضات
قبلی را در مورد دنبالههای مثلثاتی عنوان کرد:
روشی که نویسنده به چنین معادلاتی رسیده خالی از اشکال نیست و تحلیل او برای
یکپارچه کردن و عمومیت دادن به آنها، هنوز نیاز به کار دارد.
طبیعی بود که مقالاتی که برنده جایزه میشوند منتشر شوند، ولی کمیته بدلیل
نقدی که به این مقاله وارد شده بود از چاپ آن خودداری کرد.
در سال 1817 فوریه بعنوان عضو آکادمی علوم پاریس برگزیده شد. پنج سال بعد دبیر
بخش ریاضی آکادامی، ژان دِلامبر (Jean Delambre) درگذشت. فرانسو آرگو، بیو، و فوریه برای
جانشینی او نامزد شدند. آرگو از دور خارج شد و فوریه با اکثریت بالایی به پیروزی
رسید. پس از آن آکادامی فوراً مقاله فوریه که عنوان آن ’نظریه تحلیلی گرما‘
بود و برنده جایزه شده بود را چاپ کرد. بنظر میرسید که فوریه در کمیته اعمال نظر
کرده باشد، ولی این دلامبر بود که قبلاً آن را برای چاپ فرستاده بود. با این وجود،
چنین چیزی باید موجب خوشحالی فراوانی برای فوریه شده باشد.
![]()
پدر فوریه خیاطی بود که حاصل اولین ازدواجش سه بچه بود. هنگامی که همسرش فوت
کرد، او برای بار دوم ازدواج کرد، و حداقل صاحب دوازده فرزند شد، که در این میان
ژُزف فرزند نُهم بود. هنگامی که ژُزف نُه ساله بود مادرش، و چند سال بعد هم پدرش،
فوت کردند. او تحصیلات خودش را در مدرسهای آغاز کرد که توسط یک استاد موسیقی بنام
اُکسر اداره میشد. او در آنجا فرانسه و لاتین خواند، و درسش بسیار خوب
بود. در 1780، او در سن 12 سالگی به مدرسه نظامی سلطنتی رفت. ادبیات او خوب بود،
ولی سیزده سالش که بود استعداد واقعی او شکوفا شد، و آن چیزی نبود جز ریاضیات. او
کتب درسی پیشرفته ریاضی را میخواند، و در طول یک سال شش جلد از کتابهای درسی اتین
بزو (Étienne Bézout) را خوانده بود.
او که قصد داشت کشیش شود، در 1787 به صومعه بندیکتین رفت، ولی همچنان مجذوب
ریاضیات بود. او تصمیم گرفت وارد کارهای مذهبی نشود و در سال 1789 صومعه را ترک
کرد، و در همین زمان مقالهای را درمورد معادلات جبری به آکادامی فرستاد.
یک سال بعد، او در مدرسهای که قبلاً درس میخواند بعنوان معلم مشغول بکار شد. در
سال 1793 با عضویت او در کمیته انقلابی، اوضاع کمی پیچیده شد. در آنجا او خودش را
وقف آرمانهای انقلابی کرد. ولی خشونتی که در روزهای اولیه انقلاب فرانسه وجود
داشت او را آزرده کرد، و سعی کرد استعفاء دهد. از لحاظ سیاسی اینکار ممکن نبود، و
ناچاراً او به انقلاب گره خورده بود. کشمکشهای جناحی در میان انقلابیون معمول
بود، و فوریه نیز طرفدار یکی از این دستهها در اورلئان شده بود. این به دستگیری
او منجر شد، و انتظار میرفت که اعدام شود. در همان زمان، یکی از مهمترین چهرههای
انقلاب، یعنی ماکسیمیلیان روبسپیر (Robespierre)، با گیوتین
گردن زده شد. بعد از آن فضای سیاسی تغییر کرد، و فوریه هم آزاد شد.
تحت هدایت بهترین ریاضیدانان آن زمانِ فرانسه، کارهای ریاضی فوریه شکوفا شدند.
هنگامی که در سال 1795 مدرسه اکول نورمال باز شد، او جزء اولین
دانشجویانی بود که به آنجا رفت. او در کلاسهای لاگرانژ (Lagrange)، که
بعنوانی یکی از دانشمندان برجسته اروپا شناخته میشد، شرکت میکرد، و همینطور در
کلاسهای لوژاندر (Legendre)، که خیلی او را تحت تاثیر قرار نداد، و کاسپارد مونژ (Gaspard Monge).
او در جایی مشغول بکار شد که بعداً به پلی تکنیک معروف گشت. در آنجا سابقه
او برایش دردسرساز شد و بار دیگر دستگیر و به زندان افتاد. ولی به دلایلی که زیاد
معلوم نیست بزودی آزاد شد. در سال 1797 اوضاع تغییر کرد و او وارث کرسی لاگرانژ در
آنالیز و مکانیک شد.
در این زمان ناپلئون مصر را اشغال کرده بود. فوریه همراه با مونژ و چند تن
دیگر بعنوان مشاوران علمی به ارتش او پیوستند. پس از مدتی دوره فتوحات ناپلئون رو
به افول گذاشت، و هورِیشیو نلسون (Horatio Nelson) ناوگان
فرانسه را در نبرد نیل نابود کرد، و این باعث شد تا ناپلئون در مصر گیر بیافتد.
در این مدت فوریه چند منصب مدیریتی گرفت، یک نظام آموزشی برپا کرد، و به تحقیقات
باستان شناسی پرداخت. او عضو موسسِ بخش ریاضی انجمن قاهره بود، که گزارشهای
کشفیات علمی را سازمان میداد. فوریه کسی بود که ژان-فرانسوا شامپولیون
را
با سنگ روزتا (Rosetta
Stone) آشنا کرد، و همین باعث شد تا او راز
زبان هیروگیریف مصری را کشف کند.
در 1799 تاپلئون ارتش خودش را در مصر رها کرد و به پاریس بازگشت. بدنبال او فوریه
هم در سال 1801 به پاریس و کار تدریس خودش برگشت. ولی ناپلئون چون دید فوریه مدیر
قابلی است، تصمیم گرفت او را به مدیریت بخش ایزر (Isère) بگمارد. این پیشنهادی بود که
فوریه نمیتوانست آن را رد کند، و آن را با بیمیلی پذیرفت. بنابراین به گرنوبل
نقل مکان کرد. او در آنجا بر خشک کردن مردابها، و ساخت بزرگراهِ گرنوبل-تورین
نظارت داشت. او همچنین بر روی کتاب بزرگ ناپلئون بنام، تشریح مصر که در
1810 چاپ شد کار کرد. فوریه در 1816 به انگلستان رفت، ولی خیلی زود به فرانسه
بازگشت تا دبیر دائمی آکادامی پاریس شود. زمانی که او در مصر بود با مشکل گرمازدگی
دست به گریبان بود، مشکلاتی که حتی پس از بازگشت به فرانسه هم ادامه داشت، و مدام
دچار تنگی نفس میشد. در سال 1830 او از پلهها سقوط کرد، و شرایطش بدتر شد، و کمی
بعد فوت کرد. نام او یکی از 72 نامی است که در برج ایفل حک شده. ولی تا آنجا که به
ریاضیات مربوط است، اوج دوران فوریه زمانی بود که در گرنوبل اقامت داشت، زیرا در
همانجا بود که تحقیقات مهم خودش بر روی گرما را انجام داد.
![]()
معادلات فوریه بصورت نمادی جریان گرما را در یک میله رسانا (مثلاً یک میله
فلزی) توصیف میکنند. اگر قسمتی از میله از اطراف آن داغتر باشد، گرما به نواحی
مجاور پخش میشود. اگر قسمتی از میله از نواحی مجاور سردتر باشد، گرما به آنجا میآید.
هرچقدر اختلاف گرما بیشتر باشد، گرما هم سریعتر پخش میشود. نرخی که گرما جریان مییابد،
همچنین تعیینکننده این است که میله با چه سرعتی سرد میشود. معادلات گرمای فوریه
توصیف کننده رابطه میان این دو روند هستند.
در ابتدا قسمتهای مختلف میله میتوانند به دماهای مختلفی کاهش یا افزایش پیدا
کنند، که این یک توزیع گرما را ایجاد میکند. حل این معادلات نشان میدهد که چگونه
توزیع اولیه گرما با گذشت زمان در طول میله تغییر میکند. شکل دقیق معادله، فوریه
را به یک جواب ساده هدایت کرد، که حالتی خاص بود. اگر توزیع دمای اولیه یک منحنی
سینوسی باشد، که یک دمای حداکثر در وسط دارد، آنگاه دما با گذشت زمان دارای یک
نمودار یکسان است، ولی بصورت نمایی به سمت صفر تنزل میکند. ولی آنچه فوریه
حقیقتاً میخواست بداند این بود برای نمودار دمای اولیه چه اتفاقی میافتاد. مثلاً
فرض کنید که در ابتدا میله تا نیمه طولش داغ شود، و در طول نیمه دیگرش سردتر
بماند. آنگاه نمودار اولیه به شکل یک موج مربعی است، و این یک منحنی سینوسی نیست.
چگونه از سینوسها و کسینوسها یک موج مربعی بدست میآید. چپ: اجزاء موجهای سینوسی. راست: مجموع آنها که
تشکیل یک موج مربعی را داده. در اینجا اولین جملات دنباله فوریه نشان داده شدهاند.
هر چه تعداد جملات بیشتر شود، موج مربعی بهتری ساخته خواهد شد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

کارل فردریش گاوس (Carl Friedrich Gauss): تولد: 30 آوریل 1777 میلادی، آلمان. وفات: 23 فوریه 1855.
سیام
ماه مارس 1796 بود و کارل فردریش گاوس جوان دو دل بود که آیا زبان بخواند یا ریاضیات. او حالا
موفقیت بزرگی را حاصل کرده بود و با استفاده از روشهای جبری توانسته بود یک ساخت
هندسی را پیدا کند که برای بیش از دو هزار سال از زمان اقلیدس از دید ریاضیدانان
پنهان مانده بود. او با استفاده از ابزارهای سنتی، یعنی خطکش و پرگار، توانسته
بود یک هفدهضلعی منظم (heptadecagon) را رسم
کند. چند ضلعی منظم یک چندضلعی است که کلیه اضلاع، و کلیه زویای درونی آن
با هم مساویند، نه اینکه تقریباً مساوی باشند (چون رسم چنین چیزی آسان است)، بلکه دقیقاً
مساویند. کمتر کسی فرصت این را داشت تا مسئلهای را حل کند که برای بیش از دو هزار
سال لاینحل مانده بود. علاوهبراین، گرچه ریاضیات بکار رفته در حل این مسئله از
اصالت و زیبایی فوقالعادهای برخوردار است، ولی از لحاظ عملی، این مسئله کاربردی
ندارد.
چنین مسائلی اولین بار در کتاب اصول اقلیدس مطرح شدند. در آنجا طریقه
رسم یک سهضلعی منظم (یا همان مثلث متساوی الاضلاع)، یک مربع، یک پنجضلعی منظم، و
یک شش ضلعی منظم داده میشود. درباره هفت ضلعی منظم چطور؟ نه، در اینمورد هیچ چیز
ذکر نشد. البته ساخت هشتضلعی آسان است (مربعی را رسم کنید که در داخل یک دایره
قرار دارد و اضلاع آن را نصف کنید؛ سپس نیمهها را امتداد دهید تا دایره را در
چهار نقطه دیگر قطع کند، اگر این نقاط را به چهار گوشه مربع وصل کنید، یک هشت ضلعی
منظم خواهید داشت.) اگر شما بتوانید یک چندضلعی منظم را رسم کنید، آنگاه با
استفاده از روش فوق میتوانید یک چندضلعی را رسم کنید که تعداد اضلاع آن دو برابر
باشد. خوب در مورد نهضلعی چطور؟ نه، دراینمورد هم اقلیدس ساکت است. دهضلعی هم
ساده است چون دو برابر پنج است. باز خبری از یازدهضلعی نیست. دوازدهضلعی هم دو
برابر ششضلعی است. سیزده یا چهارده ضلعی چطور؟ نه، خبری از آنها هم نیست. پانزدهضلعی
را میتوان با ترکیب یک سهضلعی و یک پنجضلعی ساخت. شانزده ضلعی هم که دو برابر
هشت ضلعی است.
اقلیدس فقط تا همین جا پیش میرود. سه، چهار، پنج، و کلیه مضربهای آنها در
توانهای عدد 2. هفده چطور؟ هنر گاوس در کشف همین مورد بود. حتی بهتر از
این، او نشان داد که این غیر ممکن است که با استفاده از خطکش و پرگار بتوان
چندضلعیهای منظم هفت، نه، یازده، سیزده، و چهارده ضلعی رسم کرد. دلیل سادهای
برای اینکار وجود دارد (هر چند اثبات آن اصلاً ساده نیست). هفده یک عدد اول است، و
اگر یک را از آن کم کنیم به شانزده میرسیم، که توانی از دو است.
گاوس فهمید که کلید رسم یک چندضلعی منظم توسط خطکش و پرگار در همین است. او
در دفترچه کوچکی که داشت به زبان لاتین نوشت ’Principia
quibus innititur sectio circuli, ac divisibilitus eiusdem geometrica in
septemdecim partes etc. ‘ یعنی میتوان دایره را به هفده بخش مساوی تقسیم
کرد. این اولین مورد از 145 موردی است که بعداً او آنها را کشف کرد و در این
دفترچه یادداشت کرد، که برخی از آنها بصورت اختصار، و برخی دیگر رمزی نوشته شده
بودند.
پس زبان یا ریاضیات؟
در این مورد جای هیچ تردیدی نبود.
![]()
گاوس در خانواده فقیری بدنیا آمد. پدرش گرهارد بعنوان یک باغبان در شهر
برونسویک شغلی گرفت و بعداً به کارهایی مثل چاهکنی و آجرچینی پرداخت. مادر
گاوس که دورِتا نام داشت، آنقدر بیسواد بود که حتی نمیتوانست تاریخ تولد
پسرش را ثبت کند. ولی او به هیچ وجه آدم کمهوشی نبود، و بخاطر داشت که پسرش در یک
روز چهارشنبه، هشت روز قبل از روز معراج بدنیا آمده بود. ولی بعدها گاوس از
همین اطلاعاتِ کم استفاده کرد تا تاریخ دقیق تولدش را تعیین کند.
استعداد ذهنی گاوس خیلی سریع آشکار شد. هنگامی که او سه ساله بود، پدرش مشغول
پرداخت دستمزد کارگرها بود. ناگهان کارل کوچک فریاد زد ”نه، پدر این درست نیست،
باید اینطوری باشد ...“ با محاسبه دوباره معلوم شد که حرف این پسر بچه درست است.
والدین گاوس که به تواناییهای بالقوه وی پی برده بودند نهایت توان خودشان را برای
به ثمر رساندن آن انجام دادند. هنگامی که گاوس هشت ساله بود، معلم آنها برای اینکه
سر بچهها را گرم کند از آنها خواست تا مجموع اعداد 1 تا 100 را
حساب کنند. اگر راز این محاسبه ساده را برای دانشآموزان برملا نکنید، میتوانید
ساعتها آنها را به محاسبات طولانی مشغول کنید، محاسباتی که احتمالاً اشتباه نیز
از کار در میآیند. دانشآموز هشتساله ما برای لحظهای پشت میزش نشست، عددی را بر
روی لوح خودش نوشت، سپس بلند شد و آن را به معلم داد. او با گویش محلی خودش به
معلم گفت ’جواب این است.‘ این راه معمولی برای ارائه جواب به معلم بود، و بیاحترامی
هم در آن نبود. همانطور که دانشآموزان دیگر مشغول بودند، و لوح آنها مملو از
محاسبه میشد، معلم نگاهی به گاوس که به آرامی روبروی میزش نشسته بود انداخت.
هنگامی که لوحها بررسی شدند، تنها جواب درست را گاوس نوشته بود.
فرض کنید که مسئله واقعاً این باشد که حاصل 1+2+3+…+99+ 100 را حساب کنید. راه
میانبر برای حل آن چیست؟ خوب شما ابتدا باید دارای یک قوه تخیل باشید تا بفهمید
واقعاً راهحل میانبری برای این مسئله وجود دارد. سپس باید این راه را پیدا کنید،
و اگر توانستید، آنگاه میتوانید از همین ترفند برای پیدا کردن حاصلِ جمعهای
پیچیدهتر نیز استفاده کنید. گمان برده میشود که گاوس در ذهن خودش اعداد را بصورت
جفتی گروهبندی کرده بود، که یکی از آنها را از ابتدا، و دیگری را از انتها انتخاب
میکرد:
1 + 100 = 101
2 + 99 = 101
3 + 98 = 101
.
.
.
و این الگو ادامه دارد (یعنی به اولی یکی اضافه میشود، ولی برای ثابت نگاه داشتن مجموع، یکی از دومی کم میگردد) تا اینکه نهایتاً به مورد زیر میرسیم:
50 + 51 = 101
ما 50تا از چنین جفتهایی، که
مجموع آنها 101 میشود، داریم، بنابراین مجموع کلی آنها عبارت
خواهد بود از: 50
× 101 = 5050. و جواب این است!
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

نیکولای ایوانوویچ
لوباچفسکی (Nikolai Ivanovich
Lobachevsky): تولد: 1 دسامبر 1792
میلادی، روسیه. وفات: 24 فوریه 1856.
برای بیش از دو هزار سال کتاب اصول اقلیدس نمونه علای توسعه منطقی در
نظر گرفته میشد. این کتاب کارش را با چند فرض ساده شروع میکرد، که بطور روشن
بیان شده بودند، و اقلیدس توانست قدم به قدم، کلِ هندسه را از همین فرضها نتیجه
بگیرد. او کارش را با هندسه صفحه شروع کرد، و سپس به هندسه فضایی پرداخت. منطق
اقلیدس چنان قانعکننده بود که نه تنها هندسه او بعنوان نمایشِ ایدآل ریاضیِ
ساختار ظاهری فضای جهان در نظر گرفته میشد، بلکه تشریح واقعی این جهان بود. صرف
نظر از هندسه کروی (هندسه سطح یک کره، که بطور گسترده از آن در دریانوردی
استفاده میشد، و هنوز هم میشود)، دیدگاه قالب در میان ریاضیدانان و دانشمندان
این بود که هندسه اقلیدسی تنها هندسه ممکن است، بنابراین ساختار فضای فیزیکی نیز
توسط همین هندسه تعیین میشود. در حقیقت هندسه کروی در مقایسه با هندسه اقلیدسی نوع
متفاوتی از هندسه نیست، بلکه همان هندسه است که به کرهای محدود شده که در فضای
اقلیدسی قرار دارد. درست به همان صورت که هندسه مسطحه همان صفحهای است که در فضای
اقلیدسی قرار دارد.
کُل هندسه آن دوران، اقلیدسی بود.
یکی از اولین کسانی که به نامعقول بودن این موضوع شک کرد گاوس بود، ولی او
تمایل چندانی به نشر چنین افکاری نداشت، و اعتقاد داشت که انتشار چنین موضوعاتی
مسائل غامضی را پیش خواهد کشید. عکسالعملهای دیگران میتواند از تهمت به نادانی
تا دیوانگی باشد. پیشکسوتِ محتاطِ ما تصمیم گرفته بود که درباره موضوعات جنجالی
اظهار نظر نکند.
نیکولای ایوانوویچ لوباچفسکی (Nikolai Ivanovich Lobachevsky) شجاعتر، بیکلهتر یا خامتر از گاوس بود. شاید هم همه اینها در
او صدق میکرد. هنگامی که او جایگزینی برای هندسه اقلیدسی پیدا کرد که
دقیقاً از همان زیربنای منطقی و زیبایی درونی برخوردار بود، او به اهمیت کارش پی
برد و ایدههای خودش را در سال 1823 در کتابی بنام هندسه چاپ کرد. در 1826 او از
گروه ریاضی-فیزیک دانشگاه کازان درخواست کرد تا درباره این موضوع سخنرانی کند، و
سرانجام متن آن در نشریه (Kazan
Messenger) منتشر شد. او همچنین آن را
برای آکادمی معتبر سنت پیترزبورگ فرستاد، ولی میخایل استردرادسکی (Mikhail Ostrogradskii) آن را رد کرد. در 1855 زمانی که لباچوفسکی کور شده بود، متن
جدیدی از هندسه-نااقلیدسی را دیکته کرد، که عنوان آن هندسهفراگیر (Pangeometry)
بود. حدود پنجاه سال بعد از مرگ لوباچفسکی، سرانجام کتاب هندسه او با عنوان (Geometriya)
چاپ شد.
حالا کشفیات برجسته او و ریاضیدان مجارستانی یانوش بویایی (János Bolyai)،
که حتی کارهایش کمتر از لباچوفسکی مورد اعتناء قرار گرفت، بعنوان شروع یک انقلاب
عظیم در سیر فکری انسان درباره هندسه و سرشت فضای فیزیکی در نظر گرفته میشود. ولی
ظاهراً این سرنوشت همیشگی پیشگامان است که درابتدا بد جلوه میکنند یا ایدههای
آنها بد تعبیر میشود. ایدههایی که برای نوآوریها آنها باید مورد احترام قرار میگرفتند،
بطور عادی بعنوان حرفهای نامعقول تقبیح میشدند، و نوآوران کمتر به رسمیت شناخته
میشدند. حتی احتمال بیشتر این بود که دیگران با آنها دشمن شوند؛ مثلاً تکامل
داروین، یا در همین دوره ما، مسئله تغییرات اقلیمی را در نظر بگیرید. بعضی اوقات
من احساس میکنم که نژاد انسان لیاقت متفکرین اصیل خودش را ندارد. هنگامی که آنها
ستارگان را به ما نشان میدهند، پیشداوری و فقدان قوه تخیل، دوباره ما را به لجن
میکشاند.
![]()
در اینمورد، بشر متحد شده بود تا بر این عقیده باشد که هندسه باید اقلیدسی
باشد. فیلسوفانی نظیر امانوئل کانت (Immanuel Kant) به تفصیل
شرح دادند که چرا چنین چیزی غیرقابل اجتناب است. این عقیده برپایه سنت دیرینی قرار
داشت که حاصل تلاشهایی بود که میخواست درک استدلالهای اقلیدس را به همه
بفهماند، و در طول نسلهای متمادی بعنوان یک آزمون فکری به دانشآموزان تحمیل شده
بودند. معمولاً آدمها برای دانشی که از طریق یک تلاش سخت بدست آمده ارزش بیشتری
قایل هستند: اگر هندسه اقلیدسی نمایانگر فضای حقیقی نبود، در اینصورت همه این تلاشهای
سخت هدر میرفت. دلیل دیگری که وجود داشت خط فکری فریبندهای بود که این استدلال
را تقویت میکرد که هندسه اقلیدسی تنها هندسه ممکن بود. چه چیز دیگری غیر از هندسه
اقلیدسی میتوانست وجود داشته باشد؟
برخی اوقات پرسشهای لفاظانه جوابهای لفاظانه طلب میکند، و این سئوال خاص،
که خیلی جدی گرفته شده بود، ریاضیدانان را به آبهای عمیقی کشاند که خلاصی از آنها
ساده نبود. محرک اولیه این مشکل یکی از ویژگیهای کتاب اصول اقلیدس بود که ناقص
بنظر میرسید. اقلیدس هندسهاش را با فرض گرفتن چند اصلِ سادهِ اثبات نشده، که
صراحتاً بیان میشد، بصورت منطقی توسعه داد. از آن پس، بقیه چیزها قدم به قدم از
این اصول نتیجهگیری میشوند. بیشتر فرضها ساده و معقول بودند، مثل اینکه ’کلیه
زاویههای قائمه با هم مساوی هستند‘. ولی یکی از آنها چشمگیر و ناخوشایند بود:
اگر یک پاره خط دو خط را قطع کند و دو زاویه درونی در سمتی تشکیل دهد که مجموع
آنها از دو زاویه قائمه کمتر باشد، و اگر این دو خط بصورت نامتناهی امتداد یابند،
آنگاه این دو خط در همان سمتی که مجموع زوایای درونی آنها کمتر از دو زاویه قائمه
است همدیگر را قطع میکنند.
گزاره فوق بعنوان اصل توازی شناخته میشود، زیرا در واقع به خطوط موازی مربوط
است. هنگامی که دو خط موازی باشند، آنها هیچ وقت یکدیگر را قطع نمیکنند. در
اینحالت اصل توازی به ما میگوید که مجموع دو زاویه درونی باید دقیقاً برابر دو
زاویه قائمه (180 درجه) باشد، و اگر اینطور باشد، این دو خط با هم موازی هستند.
خطوط موازی اساسی و آشکار هستند. برای مشاهده این مورد کافیست به یک کاغذِ خطکشی
شده نگاه کنید. واضح است که چنین خطوطی وجود دارند، و البته بدلیل اینکه فاصله
خطوط مساوی است، آنها هیچوقت یکدیگر را قطع نمیکنند. آیا در اینجا اقلیدس تلاش
زیادی میکرد تا چیزی را بگوید که خیلی واضح بود؟ یک احساس کلی بوجود آمد که باید
امکان این وجود داشته باشد که بتوان اصل توازی را از بقیه اصول موضوعه اقلیدس
نتیجه گرفت. حقیقتاً افراد زیادی بر این باور بودند که آنها این کار را کردهاند
ولی وقتی ریاضیدانان مستقل اثباتهای فرضی آنها را بررسی کردند، همیشه در جایی یک
اشتباه پیدا میشد، یا بدون آنکه شخص حواسش باشد، چیزی دیگری فرای اصول موضوعه فرض
گرفته شده بود.
ریاضیدان ایرانی عمر خیام در قرن یازدهم میلادی اولین تلاشها
را برای حل این موضوع کرد. من قبلاً در فصل 5 به کارهای او در زمینه حل معادله درجه سوم اشاره کردم، ولی
این تنها چیزی نبود که او در چنته ریاضی خودش داشت. در کتاب ’ شرح مشکلات موجود
در کتاب اصول اقلیدس‘ خیام بر اساس تلاشهای اولیه حسن ابن هیثم خواست تا اصل توازی را
اثبات کند. او بر اساس موارد منطقی همه این ’اثباتها‘ را رد کرد، و آنها را با
استدلالی جایگزین کرد که اصل توازی را به یک عبارت شهودیتر کاهش میداد.
یکی از شکلهای اصلی او مسئله را مشخص میکند. این را میتوان بعنوان تلاش
برای ساختن یک مستطیل در نظر گرفت- که ما آن را یک چیز کاملاً ساده میپنداریم. یک
خط مستقیم، و دو خط مساوی که با این خط زاویه قائمه میسازند را رسم کنید. نهایتاً
انتهای این دو خط را با یک خط مستقیم به هم متصل کنید تا ضلع چهارم بدست آید. کار
تمام است!
در اینجا AC=BD و زوایای A و B
قائمه هستند. آیا DC مستطيل را کامل میکند؟
ولی آیا همینطور است؟ ما از کجا میدانیم که شکل حاصله یک مستطیل است؟ در یک
مستطیل کلیه زاویهها قائمه هستند، و اضلاع روبرو با هم مساویاند. در نمودار خیام
ما میدانیم که دو زاویه قائمه هستند و یک جفت از اضلاع با هم مساویند. در مورد
بقیه چطور؟
درست است، بنظر میرسد که ما یک مستطیل رسم کردهایم، ولی این بخاطر
این است که ما برای پیشفرض ذهنی خودمان از هندسه اقلیدسی استفاده کردهایم. و به
واقع در هندسه اقلیدسی ما میتوانیم ثابت کنیم که CD=AB و زوایای C و D نیز قائمه هستند. ولی چنین استنتاجی به
... اصل توازی نیاز دارد. این زیاد تعجب برانگیز نیست، زیرا ما انتظار
داریم CD با AB موازی باشد. اگر شما بخواهید اصل
توازی از بقیه اصول موضوعه اقلیدس نتیجه بگیرید، باید ثابت کنید که خیام بدون
توسل به اصل توازی یک مستطیل رسم کرده. در حقیقت خیام متوجه شد که اگر شما
بتوانید چنین اثباتی را پیدا کنید، کار تمام است. اصل توازی خودش فوراً به دنبال
این خواهد آمد. با دوری از دام اثبات اصل توازی، خیام بطور صریح آن را با فرض
مشابهای جایگزین کرد ’خطوط مستقیم همگرا همدیگر را قطع میکنند، و غیر ممکن است
که دو خط مستقیم همگرا در همان جهتی که همگرا هستند، واگرا شوند.‘ و او بخوبی آگاه
بود که این یک فرض است.
جیووانی ساکری (Giovanni Saccheri)، احتمالاً
بطور مستقل، از شکل خیام استفاده کرد تا اصل توازی را اثبات کند. کتاب او بنام ’
اقلیدس مُبرا از هر خطا‘ در سال 1733 چاپ شد. او اثبات خودش را به سه حالت
تقسیم کرد، که به این بستگی داشت که زاویه C در شکل قائمه باشد، حاد
باشد (کمتر از 90 درجه)، یا منفرجه (بزرگتر از 90 درجه). ساکری اثبات کرد که در هر
یک از اشکال وضعیت زاویه C هر
چه باشد، برای همه اشکال همنوع یک چیز اتفاق میافتاد. زویا یا همه قائمه هستند،
یا همه حاد، و یا همه منفرجه. بنابراین برای هر مستطیل سه حالت وجود ندارد، بلکه
رویهم رفته سه حالت وجود دارد. این قدم مهمی به جلو بود.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

اواریست گالوا (Évariste Galois): تولد: 25 اکتبر 1811،
فرانسه. وفات: 31 می 1832.
در
چهارم ماه ژوئن 1832 روزنامه فرانسوی Le Precursor واقعه مهیجی
را گزارش داد، که در آن زمان به هیچ وجه غیرعادی نبود:
”پاریس، یکم ژوئن – روز گذشته در طی یک دوئل اسفناک،
جوانی که بنظر آینده درخشانی داشت، ولی اخیراً شهرت او بیشتر تحتالشعاع فعالیتهای
سیاسی او قرار گرفته بود، کشته شد. اواریست گالوای جوان ... با یکی از دوستان
قدیمی خود، که مانند او عضو جامعه دوستان خلق بود و محاکمه نیز شده بود،
درگیر نزاعی مهلک شد. آنگونه که گفته میشود دلیل دعوا یک ماجرای عشقی بوده. از
طپانچه بعنوان سلاح دوئل استفاده شده، ولی چون دو حریف از دوستان قدیمی یکدیگر
بودهاند سلاحهای یکدیگر را بررسی نکردهاند. آنها در فاصله کمی نسبت به هم
ایستاده، و از همین فاصله نیز شلیک کردهاند. تنها یکی از تپانچهها آتش شده. بدن
گالوا با گلولهای که حریفش شلیک کرده کاملاً سوراخ شده؛ او را به بیمارستان کوشین
منتقل کردند و حدود 2 ساعت بعد فوت کرد. او 22 ساله بود. حریف وی L.D کمی از او جوانتر بود.“
شب قبل از دوئل، گلوا مشغول نوشتن خلاصه تحقیقات ریاضی خودش بود، که تمرکز آن
بر روی کاربرد مجموعهای از جایگشتها بود که او آنها را ’گروه‘ (group) مینامید،
تا مشخص شود که آیا معادلات جبری توسط فرمولها قابل حل هستند یا نه. او همچنین
ارتباط میان این ایده و توابع خاصی که بنام انتگرالهای بیضوی (Elliptic integrals)
شناخته میشوند را شرح داد. نتایجی که او حاصل کرد حاکی از آن بود که معادلات درجه
پنجم قطعاً هیچ فرمولی ندارند. این سئوالی بود که تا پیش از اینکه گابریل روفینی (Gabriel Ruffini) یک
پاسخ طولانی به آن دهد، قرنها ریاضیدانان را بخودش مشغول کرده بود. البته بعداً نیلز هنریک آبل (Niels Henrik Abel) پاسخ سادهتری را برای آن ابداع کرد.
علیرقم تلاش تاریخ نگاران برای تعیین مسیر واقعی حوادث، تا به امروز اسطورههای
زیادی درباره گالوا مطرح است. برای مثال، شخصی که حریف او بوده چه کسی بود؟ مقاله
روزنامه مذکور در اینمورد نامعتبر است، زیرا سن او را درست ننوشته، و بقیه داستان
نیز مبهم روایت شده. ولی آنچه روشن است، اهمیت دستآوردهای ریاضی اوست. مفهوم گروهِ
جایگشت یکی از اولین قدمها بسوی نظریه گروهها بود. بعداً معلوم شد که این
کلید اصلی تقارنِ ریاضی است، و حتی امروز هم یکی از حوزههای تحقیقاتی مهم را
تشکیل میدهد. حالا گروهها مرکز بسیاری از حوزههای ریاضیات، و جزء تفکیک ناپذیر
فیزیکِ ریاضی هستند. آنها کاربردهای مهمی در شکلگیری الگوها در بسیاری از حوزههای
علوم فیزیکی و زیستی دارند.
![]()
پدر اواریست، که نیکلاس نام داشت، یک انقلابی بود که پس از به تخت نشستن
مجدد لویی هیجدهم در سال 1814، شهردار شهر بورگلارن شد. مادرش آدلاید،
دختر تحصیل کرده یک مشاور حقوقی بود. او علوم دینی و ادبیات کلاسیک خوانده بود، و
تا سن دوازده سالگی به اواریست در خانه درس میداد. در 1823 او را به کالج
لویی-لو-گراند فرستادند. او در زبان لاتین شاگرد اول شد، ولی حوصلهاش سر رفت و
برای رهایی از آن به ریاضیات پناه برد. او آثار پیشرفتهای از قبیل کتاب مقدمات
هندسه اثر لوژاندر و کارهای اولیه آبل و لاگرانژ درباره حل معادلاتِ چندجملهای
توسط رادیکالها را مطالعه میکرد. اینها به فرمولهایی دلالت میکند که فقط شامل
ضرایب معادله، و چهار عمل اصلی، و استخراج ریشههای (دوم، سوم، یا بالاتر) باشند.
بابِلیان توانستند معادلات درجه دوم را توسط رادیکالها (جذرگرفتن) حل کنند، و پس
از گذشت حدود 3000 سال، ریاضیدانان دوره رنسانس توانستند همین کار را برای معادلات
درجه سوم و چهارم انجام دهند. حالا معلوم شده بود که ظاهراً چنین روشهایی برای
معادلات درجات بالاتر جواب نمیدهد. آبل در سال 1824 اثبات کرد که بطور کلی
معادلات درجه پنجم را نمیتوان توسط رادیکالها حل کرد، و در سال 1826 اثبات
کاملتری را برای آن ارائه داد.
گالوا توصیه معلم ریاضی خودش را نادیده گرفت و بدون اینکه آمادگی داشته باشد،
در کنکور ورودی دانشگاه پلیتکنیک شرکت کرد. جای تعجب هم نبود که در آن آزمون رد
شد. در 1829 او مقالهای را در مورد نظریه معادلات به آکادامی پاریس فرستاد، ولی این
مقاله در آنجا بلاتکلیف ماند. گالوا از این بعنوان نشانهای از نادیدهگرفتن عمدی
نبوغ خودش برداشت کرد، ولی این فقط میتوانست از روی بیدقتی باشد. این سال بدی
برای او بود. کشیش دهکده امضاء یک سند دروغین را به پدر گالوا نسبت داده بود، و
بدنبال یک نزاع سیاسی که با این کشیش داشت، پدرش خودکشی کرد. مدت کوتاهی پس از آن
برای بار دوم سعی کرد که در آزمون ورودی پلیتکنیک شرکت کند، که اینبار هم رد شد.
در عوض او به دانشگاه رتبه پایینتری بنام اکول نورمال رفت. دروس ریاضی و
فیزیک او خوب بود، ولی ادبیاتش تعریفی نداشت. او در پایان سال 1829 در رشته علوم
فارغالتحصیل شد. چند ماه بعد نسخه جدیدی از کارهایش درباره معادلات را برای شرکت
در جایزه بزرگ به آکادامی پاریس فرستاد. فوریه که دبیر آکادامی بود، دستنوشتههای
او را به خانه برد، ولی تا پیش از اینکه درباره مقاله او گزارشی بدهد فوت کرد. بار
دیگر کارهای گالوا گم شد، و بازهم گالوا آن را نشانهای از خصومت جامعهِ حاکم با
خودش برای ندادن جایزهای که آن را مستحق خودش میدانست قلمداد کرد. چنین روایتی
با دیدگاههای انقلابی او همخوانی داشت، و عزم او را در پیوستن به نیروهای انقلاب
محکمتر کرد.
هنگامی که فرصتی حاصل شد، گالوا آن را از دست داد. در 1824 شارل دهم
جانشین لویی هجدهم شد، ولی شاه در سال 1830 با کنارهگیری روبرو شد. برای
جلوگیری از این مورد، او به سانسور مطبوعات روی آورد، ولی مردم در اعتراض به آن
شورش کردند. بعد از سه روز آشوب، بر سر یک نامزد توافق شد. این شخص لویی فیلیپ،
دوک اورلئان، بود که شاه شد. ولی مدیر اکول نورمال دانشجویانش را در آنجا
حبس کرد. ولی اینکار به مذاق گالوا که طرفدار انقلاب بود خوش نیامد. او طی نامه
تندی که در روزنامه دانشکاه چاپ شد به مدیر حمله کرد. گالوا امضاء خودش را پایین
نامه گذاشته بود، ولی ویرایستار روزنامه آن را حذف کرد. مدیر دانشگاه به بهانه
اینکه گالوا یک نامه بینام و نشان نوشته او را اخراج کرد. پس از آن گالوا به یک
شبهنظامی، بنام توپخانه گارد ملی پیوست، که پر از افراد انقلابی بود. طولی
نکشید که پادشاه این گروه را بعنوان یک تهدید امنیتی منحل کرد.
در ژانویه 1831 گالوا برای بار سوم مقالهای را در مورد نظریه معادلات خودش به
آکادامی فرستاد. پس از دو ماه که گذشت و پاسخی دریافت نکرد، او به مدیر آکادامی
نامهای نوشت و از او علت تاخیر را پرسید، ولی باز هم پاسخی دریافت نکرد. وضعیت
ذهنی او هر روز پریشانتر میشد، و تقریباً به آدمی پارانویید (همه دشمنانگار)
بدل شده بود. سوفی ژرمن (Sophie
Germain)، که یک زن ریاضیدان برجسته بود،
درباره گالوا به لیبری اینچنین مینویسد: ”آنها میگویند که او کاملاً دیوانه
شده، و من میترسم که این واقعیت داشته باشد.“ در آوریل همان سال نوزده تن از افراد
توپخانه گار ملی تلاش کردند تا دولت را سرنگون کنند، ولی هیئت منصفه آنها را تبرئه
کرد. به همین مناسبت، با حضور 200 تن از جمهوریخواهان جشنی برگزار شد. در آنجا
بود که گالوا در یکی از دستانش جام شراب، و در دست دیگرش خنجر بدست گرفت و فریاد
میزد. روز بعد او را به جرم تهدیدِ پادشاه بازداشت کردند. او به رفتار خودش
اعتراف کرد، ولی به دادگاه گفت که او که میخواسته به سلامتی پادشاه بنوشد. این
باعث شد تا هیئت منصفه او را تبرئه کند.
در ماه جولای آکادامی نظر خودش را در مورد مقاله گالوا اعلام کرد: ”ما تلاش
زیادی کردیم تا اثبات گالوا را درک کنیم. استدلال او به اندازه کافی روشن و بالغ
نیست تا ما بتوانیم درمورد صحت آن قضاوت کنیم.“ داوران یک نقد ریاضی را نیز مطرح
کرده بودند، که کلاً معقول هم بود. آنها انتظار داشتند که به آنها گفته شود برحسب
ضرایب معادله، تحت چه شرایطی معادله توسط رادیکالها قابل حل خواهد بود. گالوا شرط
ظریفی را اثبات کرده بود، ولی این شامل جوابها میشد. این یعنی هر جواب میتواند
بصورت تابع گویایی از دو جواب دیگر بیان شود. حالا معلوم شده که هیچ معیار سادهای
که بتواند بر حسب ضرایب معادله بیان شود وجود ندارد، ولی آن زمان کسی از آن خبر
نداشت.
گالوا بسیار خشمگین شد. او در روز باستیل در حالی که سرتاپا
مسلح بود و یونیفرم گارد ملی را پوشیده بود به همراه دوستش ارنست دوشاله در
جلو صف تظاهر کنندگان در حال راهپیمایی بود. هم پوشیدن این یونیفرم و هم تظاهرات
هر دو غیرقانونی بودند، و این دو یار انقلابی دستگیر و روانه زندان شدند. پس از
گذشت چهار ماه، گالوا محاکمه و به شش ماه زندان محکوم شد. او این زمان را با انجام
تحقیقات ریاضی سپری کرد، و هنگامی که در سال 1832 وبا شیوع پیدا کرد، او را به
بیمارستان فرستادند و سپس بطور مشروط عفو شد.
او که توانسته بود آزادی خودش را بدست آورد، درگیر یک رابطه عاشقانه با زن
جوانی شد که ما او را فقط با نام ’استفانی د.‘ میشناسیم. او به دوست دیگرش آگوست
شوالیه مینویسد: ”چطور میتوانم خود را دلداری دهم ، آن هم در زمانی که ظرف یک
ماه بزرگترین مایه شادی که هر مردی میتواند داشته باشد را از دست دادهام؟“ او
تکههایی از نامههای این زن را در دفترچهای کپی کرده که در یکی از آنها اینطور
آمده ” آقا، مطمئن باشید که دیگر چنین چیزهایی اتفاق نخواهد افتاد. شما اشتباه فرض
کردهاید و پشیمانی شما بیاساس است.“ برخی اوقات استفانی در تاریخ بعنوان یک زن
افسونگر ترسیم شده، و گفته میشود که دلیل دوئل گالوا یک مسئله ’ناموسی‘ بر سر این
زن بوده. ولی در سال 1968 کارلوس اینفانتوزی دستنوشتههای اصلی را بررسی
کرد و به این نتیجه رسید که این نام زن استفانی-فلیسی دو موتل دختر یک دکتر
بوده که خانه او در همان جایی بوده که گالوا زندگی میکرده. چنین برداشتی کمی
جنجالی، ولی محتمل بنظر میرسد.
گزارش پلیس درباره این دوئل میگوید که این یک دعوای شخصی بر سر یک زن بوده،
که میان گالوا و یک انقلابی دیگر در گرفته. در شب دوئل گالوا اینطور مینویسد:
”از تمام میهنپرستان و دوستان خود عذر میخواهم که مرا برای اینکه در راهی
غیر از میهنم کشته شدم ببخشند. من قربانی زن بدنامی شدم. در چنین جنجال مصیبتباری
است که زندگی من پایان مییابد. اه! چرا باید برای چنین چیز پوچ و حقیری مُرد ...
برای آنان که مرا کشتند طلب آمرزش میکنم، آنها مردمان با حسننیتی هستند.“
طبیعتاً دیدگاه او درمورد این زن جانبدارانه است، ولی اگر دشمنانش کل ماجرا را
طرح ریزی کرده بودند، پذیرفتن این که چرا او برای آنها طلب بخشش میکند سخت است.
حریف او در این نبرد که بود؟ سوابق بجا مانده پراکنده و درهم است. نویسنده
فرانسوی الکساندر دوما میگوید که این شخص یکی از رفقای انقلابی او بنام (Pescheux d’Herbinville) بود. که ما را به مقاله روزنامه Precursor و حروف اختصاری نام قاتل، یعنی ’L.D‘، بازمیگرداند. ممکن است ’D‘ مخفف d’Herbinville بوده باشد، ولی اگر چنین هم با شد، باز هم ’L‘ به چیز اشتباهی در مقاله اشاره میکند. تونی روثمن به این
نکته اشاره میکند که ’D‘
میتواند مخفف Duchâtelet باشد که نام یکی از دوستان گالوا بود، هرچند که هنوز ’L‘ مشکوک است. بر طبق گزارش
کالبدشکافی، دوئل با استفاده از یک طپانچه و در فاصله 25 قدمی انجام شده، ولی اگر
بخواهیم داستان روزنامه را باور کنیم، بیشتر شبیه یک رولت روسی [3]بوده.
شواهد فرعی گویایی مورد اخیر است، زیرا تیر به شکم گالوا برخورد کرده، که از فاصله
25 قدمی بدشانسی است. او که از پذیرفتن کشیش بر بالینش خوداری کرد، روز بعد بعلت
آماس صفاق درگذشت و در یک گور عادی در گورستان مونپارناس دفن شد.
![]()
روز پیش از دوئل، گالوا در نامهای به دوستش شاوالیه کشفیات خودش را خلاصه
کرد. این نامه مشخص میکرد که چگونه گروهها میتوانند به ما بگویند چه وقت یک
معادله چند جملهای میتواند توسط رادیکالها حل شود. همچنین کشفیات دیگر گالوا
درباره توابع بیضوی، انتگرالگیری توابع جبری، نیز در این نامه آمده بود. نامه
اینطور پایان مییابد:
از یاکوبی یا گوس نظرشان را بپرس، البته نه درمورد درست یا غلط بودن این
قضایا، بلکه در مورد اهمیت آنها بپرس. من امیدوارم کسانی پیدا شوند که قدر این
قضایا را بداند و آنها از این وضعیت درهم خارج کند.
خوشبختانه، بخاطر ریاضیات هم که بود، چنین کسانی پیدا شدند و اینکار را کردند.
اولین کسی که دستآوردهای گالوا را تحسین کرد ژوزف لیوویل (Joseph Liouville)
بود. در 1843 لیوویل با هیئتی که سه مقاله گالوا را رد کرده، یا آنها را گمکرده
بودند، صحبت کرد. او صحبتش را اینطور شروع کرد ’امیدوارم با اعلام این مورد که با
بررسی دست نوشتههای آقای گالوا توانستم راه حل مسئله مهمی را پیدا کنم، بتوانم
توجه آکادامی را جلب کنم، و آن اینکه آیا برای حل هر معادلهای میتوان از رادیکالها
استفاده کرد یا نه؟‘ بزودی یاکوبی مقالات گالوا را خواند، و - همانطور که گالوا
امیدوار بود- به اهمیت آنها پی برد. تا سال 1856، هم در فرانسه و هم در آلمان،
نظریه گالوا در دورههای کارشناسی ریاضی تدریس میشد. در سال 1909 ژول تانری،
مدیر مدرسه اکولنرمال، مراسمی برای یادبود گالوا در شهر زادگاهش بورگلارن برگزار
کرد، و در سخنانی چنین گفت: ”اجازه دهید بنام این مدرسه، که با بیمیلی او را
پذیرفت، او را درست درک نکرد، و تنها بخاطر آنچه بود او را اخراج کرد، از نبوغ
گالوا عذرخواهی کنم. او چیزی نبود جزء یکی از درخشانترین استعدادهای عصر خودش.“
خوب، مگر گالوا برای ریاضیات چه کرد؟
پاسخ کوتاه این است که او در نظریه گروهها اصول ریاضی تقارن (symmetry) را
شرح داده بود. از آن زمان تا کنون تقارن بعنوان یکی از موضوعات کلیدی ریاضیات و
فیزیک ریاضی مطرح بوده، که اساس درک ما از همه چیز را تشکیل میدهد، از نقوش
جانوران گرفته تا ملکولهای در حال ارتعاش، از شکل یک حلزون گرفته تا مکانیک
کوانتم مربوط به ذرات بنیادی.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

اُگاستا اِیدا کینگ (Augusta Ada King): تولد: 10 دسامبر 1815،
انگلستان. وفات: 27 نوامبر 1852.
خانوادش
اصلاً خانواده شادی نبود. لُرد جرج گُردون بایرون، که شاعر بود، تصور میکرد که
قرار است صاحب ’پسر شگفتانگیزی‘ شود، ولی هنگامی که همسرش آنا ایزابل
برایش دختری را بدنیا آورد به تلخی ناامید شد. نام او را اُگاستا اِیدا گذاشتند، ولی پدرش همیشه
او را ایدا صدا میکرد.
یک ماه پس از تولد ایدا، پدر و مادرش از هم جدا شدند، و چهار ماهِ بعد، پدرش
انگلستان را ترک کرد و هرگز به آنجا بازنگشت. لیدی بایرون سرپرستی دخترش را بدست
گرفت و ارتباط با لرد بایرون را ممنوع کرد، ولی بعدها ایدا به فعالیتهای پدر و
محل زندگی او علاقهمند شد. او به سراسر اروپا سفر کرد، هفت سال را در ایتالیا
سپری کرد، و هنگامی که ایدا هشت ساله بود، در اثر ابتلاء به مرض ناشناسی درگذشت.
بعدها ایدا وصیت کرد که پس از مرگش در کنار پدرش دفن شود، خواستهای که به آن عمل
شد.
آنابل فکر میکرد که شوهرش یک دیوانه است، دیدگاهی که با توجه به رفتار خشونتآمیزی
که او داشت معقول بنظر میرسید. بطور غیر مستقیم، همین باعث شد تا ایدا به ریاضیات
علاقمند شود. مادرش در ریاضی استعداد داشت و به این موضوع علاقه نشان میداد. ولی
تواناییهای شوهرش چیزهای دیگری بود. او در 1812 در نامهای به زنش اینطور نوشت:
من درباره ریاضیات کاملاً با تو موافقم، و از فاصله بسیار دوری آن را تحسین میکنم
– من میدانم که دو دو تا میشود چهار تا- و اگر میتوانستم، خوشحال میشدم آن
را اثبات کنم. هرچند باید بگویم اگر به طریقی میتوانستم دو دو تا را به پنج تا تبدیل
کنم، بسیار خوشحالتر میبودم!
بنابراین از نظر آنابل، نفرت شوهرش از ریاضیات، و آموزش آن به ایدا روش مطلوبی
برای فاصله انداختن میان پدر و دختر بود. او همچنین براین باور بود که ریاضیات ذهن
را آزمودهتر و با انضباطتر میکند. علاوهبراین، او چیزهایی مثل موسیقی را نیز
در برنامه آموزش دخترش گنجاند، موضوعی که باعث میشد او مهارتهای اجتماعی پسندیدهای
را کسب کند. ظاهراً بیشتر تلاش آنابل بر روی تحصیلات ایدا متمرکز بود تا بر خود
او. ایدا بیشتر اوقاتش را یا با مادر بزرگش یا با دایه خودش میگذراند.
ایدا هم از فواید و هم از ضررهای پرورش در یک خانوانده اشرافی انگلیسی بهرهمند
شد. او توسط چندین معلم خصوصی تعلیم میدید. یکی از معلمهای او خانم لامون
نام داشت که او را به جغرافی علاقمند کرد، موضوعی که ایدا آن را به درس حساب ترجیح
میداد، بنابراین آنابل مقرر کرد که در مقابل هر درس جغرافی، او باید دو درس حساب
بگیرد. طولی نکشید که خانم لامون دیگری چیزی برای گفتن نداشت. اعضای خانواده از
این نگران بودند فشار زیادی بر روی این دختر است، و در مقابل تنبیههایی که به او
اعمال میشود مشوقهای کمتری میگیرد. معلم ریاضی آنابل شخصی بنام ویلیام فرند
بود که برای آموزش به ایدا استخدام شد، ولی او دیگر پیر شده بود و اطلاعات او نیز
درباره این موضوع بروز نبود. بجای او، در سال 1829 دکتر ویلیام کینگ
استخدام شد، ولی دانش ریاضی او نیز اندک بود. ریاضیدانان واقعی میدانستند که رشته
آنها چیزی نیست که مردم آن را از بیرون گود تماشا کنند، برای اینکه قدر آن را
بدانید باید خودتان در آن درگیر باشید. کینگ جزء کسانی بود که ترجیح میداد درباره
ریاضیات بخواهد. ضمناً ایدا از یک سری از مشکلات جسمی رنج میبرد، از جمله یک
سرخچه شدید که برای مدت طولانی با آن دست به گریبان بود.
در سال 1833 ایدا به دربار سلطنتی معرفی شد، سنتی که برای طبقه اشراف مرسوم
بود. ولی در طول چند ماه رویداد مهمی دیگری در زندگی او اتفاق افتاد. او به یک
مهمانی رفت و با یک ریاضیدان اصیل، ولی نامتعارف، بنام چارلز بابیج (Charles Babbage)
آشنا شد. با این رویداد اتفاقی، حرفه ریاضی او بسیار پیشرفت کرد.
![]()
شاید برخورد میان این دو نسبت به آنچه که من توصیف کردم کمتر اتفاقی بود، زیرا
افراد طبقه اشراف انگلیس به همان محافلی میرفتند که دانشمندان برجسته، هنرمندان،
و تُجار در آنجا رفت و آمد داشتند. افراد برجسته در این حوزهها همدیگر را میشناختند،
و در گروههای کوچک با هم غذا میخوردند، و به فعالیتهای یکدیگر علاقه نشان میدادند.
ایدا فوراً با اشخاص برجسته دوران خودش آشنا شد، مثلاً فیزیکدانانی همچون چارلز
ویتسون، دیوید بروستر، و مایکل فارادی، و همینطور نویسنده معروف
چارلز دیکنز.
دو هفته بعد ایدا و مادرش، که او را بعنوان ملازم همراهی میکرد، ببیج را در
کارگاه او ملاقات کردند. چیزی که در آنجا بیشتر از همه جلب توجه میکرد ماشین عجیب
و پیچیدهای بود که بعداً به ماشین تفاضلی (Difference Engine) معروف شد.
بیشتر زندگی حرفهای ببیج بر روی ساخت ماشینهای قدرتمندی بود که وی امیدوار بود
بتوانند محاسبات ریاضی را انجام دهند. طرح چنین ماشینهایی اولین بار در 1812
هنگامی به ذهن او رسید که مشغول نوشتن جداول لگاریتمی بود. هرچند این جداول در آن
زمان بطور گستردهای در علوم و کشتیرانی کاربرد داشتند، ولی غالباً اشتباهاتی در
آنها بود که از خطاهای انسانی سرچشمه میگرفت. فرانسویها سعی کردند با شکست
محاسبات به جمع و تفریقِهای ساده، و سپردن آنها به افرادی که در محاسبه خبره
بودند، و بازبینی مکرر نتایج، دقت این جداول را افزایش دهند. ببیج فهمید که چنین
رویکردی برای پیادهسازی ماشینی ایدهآل است، و اگر میشد آن را درست طراحی کرد،
بسیار ارزانتر، قابلاتکاتر، و سریعتر بود.
اولین تلاش او در این راه، ماشین تفاضلی بود، که میتوان آن را بعنوان نمونه
اولیه ماشینهای حسابِ مکانیکی بحساب آورد. این ماشین میتوانست چهار عمل اصلی را
انجام دهد. هدف اصلی این بود که توسط روشهایی که بر پایه حساب تفاضلات متناهی
قرار داشتند، بتواند توابع چندجملهای، مثل مربعات و مکعبات و یا موارد مشابه
پیچیدهتر آنها، را حساب کند.
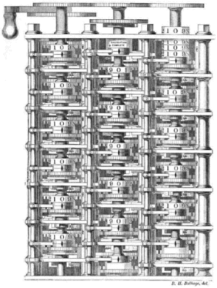
بخش کوچکی از ماشین تفاضلی
ببیج.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

جورج بول (George Boole):
تولد: 2 نوامبر 1815، انگلستان. وفات: 8 دسامبر 1864.
هنگامی
که جورج بول16 ساله بود تصمیم گرفت یک کشیش انگلیکان شود، ولی پدرش،
که یک کفاش بود، ورشکسته شد و او مجبور شد نان آور خانه شود. کار در کلیسا دیگر در
این وضعیت معقول نبود، زیرا حقوق کشیشان انگلیسی بسیار اندک بود. اعتقاد او نسبت
به اصول تثلیث مقدس[4]
نیز درحال کاهش بود، و بیشتر به سمت یکتاپرستی یعنی ’ اعتقاد به یک خدای واحد‘ سوق پیدا میکرد. بنابراین محال بود بدون
اینکه عذاب وجدان داشته باشد بتواند به سی و نه اصل کلیسای انگلستان سوگند بخورد.
مناسبترین (و شاید تنها) شغلی که با توجه به سابقه و استعدادش میتوانست بگیرد
معلمی بود، و در 1831 در مدرسه آقای هایام در دانکستر، که حدود 60
کیلومتر با زادگاهش فاصله داشت، به عنوان دستیارِ معلم استخدام شد. در اواسط قرن
نوزدهم این فاصله زیادی محسوب میشد، و او دلتنگ خانوادهاش بود. در یکی از نامههایی
که او نوشته به این اشاره میکند که ’هیچکس در دانکستر نمیتواند بخوبی مادرش کیک
انگور درست کند‘. چنین حرفی ممکن است تنها نوعی قدردانی باشد، ولی او در سراسر
زندگیش از سرنوشت خودش شکایت داشت. تمایلات او به عقاید وحدانی، همراه با علاقهای
که به حل مسائل ریاضی داشت موجب خشم برخی از والدین دانشآموزانی شده بود که پیرو
سرسخت کلیسای مِتُدیست بودند. آنها از این بابت به مدیر مدرسه شکایت بردند.
هرچند که آقای هایام از عملکرد بول بعنوان یک معلم راضی بود، ولی با بیمیلی او را
اخراج کرد.
بول در کنار کیک انگوری مادرش و بحثهای فرقهای، هرچه بیشتر خودش را در
ریاضیات غرق کرد، و مطالعاتش را بدون معلم ادامه داد. او ابتدا بر خدمات رایگان،
مثل کتابخانه تکیه داشت، ولی کتابخانه منحل شد و بول مجبور شد کتابهای درسی خودش
را خریداری کند. او کتاب حساب دیفرانسیل و انتگرال نوشته سیلوستر لاکرو
(Sylvestre Lacroix) را
خرید.
او بعداً از خرید این کتاب که تا حدی قدیمی بود پشیمان شد، ولی مطالعه این
کتاب به او اعتماد لازم برای سنجش تواناییهایش را داد. یکی از پیامدهای خواندن
این کتاب ایدهای بود که بعداً در سال 1833، هنگامی که از کنار یک مزرعه میگذشت،
به ذهن او خطور کرد، و آن امکان بیان عبارات منطقی بصورت نمادین (سَمبُلیک)
بود. سالها طول کشید تا او این ایده را بخوبی بسط دهد. اولین کتابی که او در
اینباره نوشت’ تحلیل ریاضی منطق، رسالهای درباب حساب استدلال استنتاجی‘
بود که در سال 1847 منتشر کرد. آگوستاس دِ مورگان
که
بول اغلب با وی مکاتبه داشت، او را تشویق کرد که کتاب جامعتری را در اینمورد
بنویسد. اساساً علایق او و بول درهم آمیخته بودند. بول به نصیحت دِ مورگان عمل کرد
و در 1854 شاهکار خودش بنام تحقیقاتی بر روی قوانین تفکر را منتشر کرد. در
این کتاب او منطق ریاضی (mathematical
logic) را ایجاد کرد، و چیزی را بنیان نهاد
که نهایتاً به پایه نظری علم کامپیوتر بدل شد.
![]()
پدر جورج، که جان نام داشت، از یک خانواده قدیمی لینکلنشایری آمده بود
که همه اهل کشاورزی و تجارت بودند. او کفاش شد، و آنجا را به مقصد لندن ترک کرد، و
امیدوار بود که کارش در آنجا بگیرد. او تنها در یک زیرزمین تاریک کار میکرد، و
اوقات دلتنگی خودش را با مطالعه زبان فرانسه، علوم، و ریاضیات، و خصوصاً طراحی
تجهیزات اپتیکی، پر میکرد. او با خدمتکاری بنام مری جویس آشنا شد و سپس با
او ازدواج کرد، و پس از شش ماه آنها به لینکلن بازگشتند، جایی که جان یک مغازه
کفاشی باز کرد. آنها بچه میخواستند، ولی ده سال طول کشید تا اولین فرزند آنها
متولد شود؛ آنها نام او را جورج گذاشتند. پس از آن، با فاصلهای کوتاهی، صاحب یک
دختر و دو پسر دیگر نیز شدند.
جان بیش از اینکه به کفاشی علاقه داشته باشد، وقتش را صرف ساختن تلسکوپها میکرد،
بنابراین از خیلی وقت پیش کارش کساد شده بود، ولی با اجاره دادن اطاق به مسافرین
امرار معاش میکرد. جورج در یک فضای علمی بزرگ شد و ذهن پرسشگری داشت. او به
ریاضیات علاقهمند بود و هنگامی که تنها یازده سال داشت یک کتاب درسی هندسهِ
شش-جلدی را تمام کرده بود (پدرش این را با مداد در داخل کتاب نوشته بود). او زیاد
مطالعه میکرد و حافظه روشنی داشت و قادر بود چیزهایی را که قبلاً خوانده بود
فوراً بخاطر بیاورد.
همانطور که اشاره شد، بول در سن 16 سالگی در مدرسه هایام معلم شد، و پس از
اینکه از آنجا اخراج شد، در سن 19 سالگی مدرسه خودش را در لینکلن باز کرد؛ سپس
تصدی آکادامی هال در ودینگتون را بهعهده گرفت. خانواده او برای
اداره مدرسه به او پیوستند. بول در طول این سالها هیچگاه از ریاضیاتِ پیشرفته
غافل نبود، و به مطالعه آثار کسانی مثل لاپلاس و لاگرانژ مشغول بود. او یک مدرسه
شبانهروزی را در لینکلن باز کرد، و مقالاتی را در نشریه تازه تاسیس مجله ریاضی
کمبریج منتشر کرد.
او در 1842 مکاتبه مادامالعمری را با دِمورگان شروع کرد. در 1844 او برنده
مدال انجمن سلطنتی شد، و در 1849 به سمت اولین استاد ریاضی در کویین کالج
ایرلند منصوب شد. در آنجا او با همسر آینده خودش مری اِورست (برادرزاده
کاشف معروف، جورج ِاورست، که قله اورست به افتخار او نامگذاری شده) آشنا
شد. آنها در 1855 با هم ازدواج کردند و صاحب پنج دختر شدند، که همه آنها شخصیتهای
برجستهای بودند؛ مری، که با ریاضیدان و نویسندهای بنام چارلز هوارد هینتون
(Charles Howard Hinton) ازدواج کرد. هینتون مردی بااستعداد، ولی بدجنس بود؛ مارگرت، که
با هنرمندی بنام ادوارد اینگرام تایلور ازدواج کرد؛ الیسیا، که تحت
تاثیر هینتون قرار گرفت و تحقیقات مفصلی را درمورد چندوجهیهای چهار-بعدی انجام
داد؛ لوسی، که اولین استاد شیمی در انگلستان بود؛ و اتِل، که با
دانشمند لهستانی ویلفرید وینیچ (Wilfrid Voynich) ازدواج کرد
و رمان معروف خرمگس (The
Gadfly) را نوشت.
![]()
در میان کارهای اولیه بول، یک کشف ساده وجود دارد که به پیدایش نظریه
تغییرناپذیرها (invariant
theory) منجر شد. این نظریه یکی از حوزههای
جبر است که بعداً به یکی از موضوعات موفق بدل شد. گاهی اوقات در مطالعه معادلات
جبری اگر متغیرهای یک فرمول با عبارات مناسبی جایگزین شوند که بصورت یک سری از
متغییرهای جدید هستند، آنگاه این فرمول میتواند سادهتر شود. اگر بتوان جواب این
معادلهِ ساده شده را برای متغیرهای جدید پیدا کرد، آنگاه میتوان جواب معادله
اصلی را از آنها استنتاج کرد. به همین روش بود که ریاضیدانان بابلی و دوران رنسانس
معادلات درجه دوم و سوم را حل میکردند.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

برنهارت ریمان (Bernhard Riemann):
تولد: 17 سپتامبر 1826، آلمان. وفات: 20 جولای 1866، ایتالیا.
برنهارت ریمان از سن بیست سالگی استعداد ریاضی
فراوان، مهارت فنی، و اصلالت کاری قابل توجهی را از خودش نشان داده بود. بعدها یکی
از استادانش بنام موریس استرن
(Moritz Stern) گفت که ’او از قبل درسهایش را از حفظ است‘. گاوس که یکی از
استادان دیگر ریمان بود، خیلی به این موارد توجهی نداشت، ولی
چیزهایی که گاوس به او درس میداد مقدماتی بودند و احتمالاً همه قابلیتهای واقعی
دانشجو را نشان نمیداد. حتی گاوس نیز خیلی زود به تواناییهای غیرعادی ریمان پیبرد،
و استاد راهنمای تز دکترای او شد. موضوع تز او آنالیز مختلط (complex analysis) بود
که برای گاوس خیلی عزیز بود. او درمورد رساله ریمان اینطور اظهار نظر کرد ’اصیل و
بطور شگرفی پربار‘، و برای ریمان منصبی را در دانشگاه گوتینگن ترتیب داد.
در آلمان دوره بعد از دکترا چیزی بود که درجهعالی (Habilitation) نامیده میشد
و مدرکی بود که برای دریافت آن باید تحقیقات عمیقتری انجام میشد و برای دارنده آن
عنوانی را فراهم میآورد که استاد خصوصی (Privatdozent) نامیده میشد،
و او کسی بود که میتوانست درسهایی را ارائه دهد و برای آنها هزینهای طلب کند.
ریمان حدود دو سال و نیم به نظریه سری فوریه پرداخت (به فصل 9 رجوع کنید)، و در این راه
قدمهای مهمی را برداشت. تحقیقات خوب جلو میرفت، ولی او کمکم به این فکر افتاد
که لقمهای را برداشته که بزرگتر از دهانش است.
مشکلی که وجود داشت کار بر روی سریهای فوریه نبود. این کاری بود که انجام
شده بود و ریمان از کیفیت و دقت آن مطمئن بود. مشکل بر سر مرحله نهایی صلاحیت برای
دریافت درجهعالی بود. نامزد دریافت این درجه باید یک سخنرانی عمومی ارائه میداد.
او سه موضوع را برای اینکار پیشنهاد داد، که دو تای آن به فیزیکِ ریاضیِ
الکتریسیته مربوط بود، و این چیزی بود که ریمان تحت نظر ویلهم وبر (Wilhelm Weber) آن
را مطالعه کرده بود، و سومی موضوع متهورانهتری بود که به بنیانهای هندسه مربوط
بود. این موضوعی بود که ریمان کمی به آن علاقه داشت ولی ایدههای آن هنوز ناقص
بودند. انتخاب میان این سه موضوع به گاوس محول شده بود که در آن زمان با وبر کار
میکرد و خیلی به الکتریسیته علاقمند شده بود. چیزی که ریمان بحساب نیاورده بود
این بود که گاوس علاقه زیادی نیز به هندسه داشت، و میخواست بداند که ریمان در
اینباره چه حرفی برای گفتن دارد.
پس حال ریمان باید آسینهایش را بالا میزد و تلاش میکرد ایدههای مبهم خودش
درباره هندسه را طوری توسعه دهد که نظر بزرگترین ریاضیدان آن زمان را به خودش جلب
کند، و این حوزهای بود که گاوس بیشتر عمرش را به آن فکر کرده بود. نقطه شروع،
نتیجهای بود که خصوصاً گاوس به آن مفتخر بود و آن را قضیه قابلتوجه
(Theorema Egregium) مینامید
به (فصل 10 رجوع کنید). این شکلِ سطحی را
مشخص میکند بدون اینکه به فضای پیرامونش اشاره کند، و همین بود که مبحث هندسه دیفرانسیل را گشود. این باعث شد که
گاوس به مطالعه ژئودزیکها (geodesics)، یعنی کوتاهترین
مسیر میان نقاط، و همچنین خمیدگیها (curvature)، که تعیین
کننده میزان خمیدگی سطح در مقایسه با سطح معمولی اقلیدسی هستند، بپردازد.
ریمان قصد داشت کُل نظریه گاوس را به روشی بنیادینی تعمیم دهد، یعنی آن را
طوری فرمولبندی کند که بجای سه-بعد، برای هر تعداد بُعدی جواب دهد. در آن زمان
تازه ریاضیدانان و فیزیکدانان شروع کرده بودند تا قدر ’فضاهای‘ هندسی که بیش از
دو یا سه بعد دارند را بیشتر بدانند. آنچه بنیان این دیدگاهِ بظاهر غیر ممکن را
تشکیل میداد، چیز کاملاً محسوسی بود، یعنی معادلاتی که دارای متغیرهای زیادی
هستند. در اینجا متغیرها نقش مختصات را بازی میکنند، بنابراین هر چه تعداد
متغیرها بیشتر باشند، ابعاد این فضای فرضی نیز بیشتر میشود.
تلاش ریمان برای توسعه چنین چیزی به یک بحران روانی منجر شد. چیزی که اوضاع را
بدتر میکرد کمک همزمان او به وبر برای درک الکتریسیته بود. خوشبختانه برهمکنش
متقابل میان نیروهای الکتریکی و مغناطیسی، ریمان را به مفهوم جدید ’نیرو‘ هدایت
کرد، که بر اساس هندسه بود، و این همان بینشی بود که حدود پنجاه سال بعد اینشتین
را به نسبیت عام هدایت کرد. دراینجا نیروها میتوانند با خمیدگی فضا جایگزین شوند.
حالا ریمان دیدگاه جدیدی داشت که میتوانست سخنرانی خودش را بر اساس آن ارائه دهد.
تا اندازهای ریمان مبانی هندسه دیفرانسیلِ نوین را بنا نهاد، او اینکار را با
مفهوم یک بسلای (manifold) چندبعدی و فاصلهای که توسط یک متریک تعریف میشود آغاز کرد. این
فرمولی برای تعیین فاصله میان کلیه نقاطی است که بسیار به هم نزدیک هستند. او کمیتهای
دقیقتری را تعریف کرد که حالا تانسور (tensor) نامیده میشوند.
او یک فرمول عمومی برای خمیدگی ارائه داد که بصورت گونه خاصی از تانسور بود، و
معادلات دیفرانسیلی را طرح کرد که ژئودزیک را تعیین میکردند. ولی او بدلیل همکاری
که با وبر داشت از این هم جلوتر رفت، و درمورد رابطه احتمالی میان هندسه دیفرانسیل
و جهان فیزیکی گمانهزنیهایی را انجام داد:
مفاهیم تجربی که اساس متریکِ فضا را تعیین میکنند، مفهوم یک جسم صُلب و یک
پرتو نور، در فاصلههای بسیار کوچک اعتبار خود را از دست میدهند. بنابراین ما
کاملاً آزاد هستیم که فرض را بر این بگذاریم که روابط متریک فضا در فاصلههای
بسیار کوچک با فرضهای هندسه مطابقت ندارن؛ و در حقیقت اگر بتوانیم، باید توضیح
سادهتری برای پدیدهها بدست آوریم.
هر چند تنها کسی که احتمالاً میتوانست سخنرانی ریمان را بطور کامل درک کند
گاوس بود، ولی با اینحال این یک پیروزی بود. اصالت کار ریمان تاثیر زیادی بر گاوس
گذاشت، و به وبر گفت که چقدر از عمق آن متعجب شده. قمار ریمان کارش را کرده بود.
چند سال بعد دیدگاههای ریمان توسط ریاضیدانان دیگری مثل ائوجنیو بلترامی (Eugenio Beltrami)، الوین کریستوفر
(Elwin Christoffel)، گریگوریو ریچی (Gregorio Ricci) و تولیو لوی-چیویتا (Tullio Levi-Civita)
بطور مفصلتری بسط داده شدند. بعداً معلوم شد تنها چیزی که اینشتین برای توسطه
نسبیت عام به آن نیاز داشت، کارهای این ریاضیدانان بود. اینشتین به نواحی بسیار
بزرگِ فضا علاقه داشت، درحالی که بینش ریمان برای فیزیک در فضاهای بسیار کوچک ریشه
داشت. با اینحال، همه اینها به سخنرانی ریمان بازمیگردد.
![]()
فردریش، پدر ریمان، یک کشیش لوتری بود که در جنگهای ناپلئونی نیز شرکت داشت.
خانواده آنها فقیر بود. مادرش شارلوت، هنگامی که ریمان خیلی جوان بود درگذشت.
او یک برادر و چهار خواهر داشت. تا سن ده سالگی پدرش به او آموزش میداد. در 1840
او به مدرسهای در هانوفر رفت، و مستقیماً کلاس سوم را شروع کرد. ریمان خیلی
خجالتی بود، ولی استعدادهای ریاضی او کاملاً نمایان بود. مدیر مدرسه به او اجازه
داد تا برای خواندن کتابهای ریاضی از کتابخانه شخصی وی استفاده کند. هنگامی که او
کتاب 900 صفحهای لوژاندر را به او قرض داد که درمورد نظریه اعداد بود،
ریمان ظرف یک هفته آن را خواند و بازگردادند.
او در سال 1846 به دانشگاه گوتینگن رفت، تا ابتدا به تحصیل الهیات بپردازد،
ولی گاوس به استعداد ریاضی او پی برد و به او توصیه کرد تا رشته خودش را تغییر
دهد، که او نیز با تایید پدرش اینکار را انجام داد. بعدها دانشگاه گوتینگن به یکی
از بهترین جاها برای تحصیل ریاضیات بدل شد، ولی در آن زمان، آنچه گاوس در آنجا
تدریس میکرد دروس مقدماتی بودند. بنابراین ریمان عازم برلین شد، و در آنجا زیر
نظر هندسهدان معروف یاکوب اشتاینر، متخصص جبر و نظریه اعداد گوستاو دریکله، و متخصص اعداد و آنالیز
مختلط فردیناند آیزنشتاین به مطالعه ریاضیات پرداخت.
در آنجا او مباحث آنالیز مختلط و توابع بیضوی را یادگرفت.
کوشی حسابان را از اعداد حقیقی به اعداد مختلط گسترش داده بود. مبحث آنالیز مختلط
هنگامی پدیدار شد که کارل وایرشتراس (Karl Weierstrass) به اعتراض
برکلی درمورد فلوکسینهای نیوتون پاسخ داد. وایرشتراس تعریف دقیقی از معنی حد را
ارائه داد. در اواسط قرن نوزدهم، یکی از مباحث داغ مربوط به آنالیز مختلط مطالعه توابع بیضوی (Elliptic functions)
بود، که یکی از کاربردهای آنها بدست آوردن طول کمانی از یک بیضی بود. این توابع
نوعی تعمیم عمیق از توابع مثلثاتی هستند. فوریه یکی از خواص اصلی این توابع، یعنی
تناوبی بودنشان را کشف کرد، بصورتی که با اضافه کردن مقدار 2π به متغیر،
مقدار تابع دوباره تکرار میشود. توابع بیضوی دارای دو تناوب مختلط هستند، و مقدار
آنها در شبکهای از متوازي الاضلاعها در صفحه مختلط تکرار میشود. آنها رابطه
زیبایی را که میان آنالیز مختلط و گروههای تقارن وجود داردند (تبدیل شبکه) را از
خودشان نشان میدهند. اثباتی که اندرو وایلز برای آخرین قضیه فرما ارائه داد
از همین ایده استفاده میکند. سر و کله توابع بیضوی در مکانیک نیز پیدا میشود.
برای مثال، آنها میتوانند فرمول دقیقی برای دوره تناوب یک پاندول بدست دهند. برای
این کار فرمول سادهتری نیز هست که در فیزیک دبیرستان ارائه میشود و برای نوسان
حول زوایههای کوچک جواب میدهد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

گئورگ کانتور (Georg Cantor): تولد: 3 مارس 1845، روسیه.
وفات: 6 ژانویه 1918، آلمان.
مفهوم
بینهایت، یعنی چیزهایی که تا ابد و بدون توقف ادامه دارند، از هزاران سال قبل انسان
را محسور کرده بود. فیلسوفان با این مسئله خیلی کلنجار زدند. خصوصاً در طول چند
قرن اخیر، ریاضیدانان از بینهایت استفاده گستردهای به عمل آوردند؛ بطور دقیقتر،
آنها تفسیرهای گوناگونی برای بینهایت ارائه میدادند که هر یک به زمینه مورد بحث
بستگی داشت. بینهایت فقط یک عدد بسیار بزرگ نیست، در واقع اصلاً یک عدد نیست،
زیرا از هر عدد مشخصی بزرگتر است. اگر ما عددی را درنظر بگیریم، برای اینکه
بینهایت باشد باید از خودش بزرگتر باشد. ارسطو (Aristotle) بینهایت را
بعنوان یک روند نامعینِ ادامهدار میدید: اگر حالا شما به هر عددی برسید، همیشه
میتوانید عددی را پیدا کنید که از این عدد بزرگتر باشد. فیلسوفان قدیم این را
بینهایت بالقوه (potential
infinity) مینامیدند.
بسیاری از ادیان هندو شیفته اعداد بسیار بزرگ بودند. از جمله آنها پیروان مذهب جین (Jainism)
هستند. برطبق آنچه در کتاب ریاضی جینها (Jain)، بنام سوریا پراجناپتی
(Surya Prajnapti) آمده، یک ریاضیدان آیندهنگر هندی در حدود 400 سال ق.م گفته که تعدا
زیادی بینهایت وجود دارند که اندازه آنها با هم متفاوت است. چنین حرفی یک یاوهگویی
صوفیانه بنظر میرسد. اگر بینهایت بزرگترین چیزی است که میتواند وجود داشته باشد،
چگونه نوعی از بینهایت میتواند از دیگری بزرگتر باشد؟ ولی در پایان قرن نوزدهم،
ریاضیدان آلمانی گئورگ کانتور (Georg Cantor) چیزی را
پایه گذاری کرد که به آن (Mengenlehre) میگفت، و حالا نظریه مجموعهها (set theory)
نامیده میشود، و از آن برای این استدلال استفاده کرد که بینهایت میتواند واقعی (actual)
باشد، و نه فقط مانند آنچه ارسطو میگفت بالقوه. در نتیجه برخی از بینهایتها از
بقیه بزرگتر هستند.
در آن موقع، بسیاری از ریاضیدانان چنین ایدهای را هنوز هم یک یاوهگویی
صوفیانه میپنداشتند. کانتور برای اقناع مخالفانش مجبور شد جدالی طولانی با آنها
داشته باشد. بسیاری از آنها در برابر کانتور از زبانی استفاده میکردند که میتوانست
امروز آنها را به دادگاه بکشاند. او از افسردگی رنج میبرد، چیزی که احتمالاً
دلیلش تمسخر روز افزونی بود که با آن روبرو بود. ولی حالا بسیاری از ریاضیدانان
پذیرفتهاند که حق با کانتور بود. درواقع در بسیاری از حوزههای ریاضیات کاربردی،
بویژه نظریه احتمالات (probability
theory)، تمایز میان کوچکترین بینهایت و
انواع بزرگتر آن، موضوعی اساسی است. در حال حاضر نظریه مجموعهها اساس منطقی تمامی
ریاضیات را تشکیل میدهد. داوید هیلبرت، که یکی از بزرگترین ریاضیدانان
تاریخ است، خیلی زود به این مسئله پی برد و نقل قول معروفی از او هست که میگوید:
”هیچکس نمیتواند ما را از بهشتی که کانتور آفریده بیرون براند.“
![]()
مادر کانتور، که ماریا آنا نام داشت، یک موسیقیدان بااستعداد بود، و
پدربزرگش فرانز بوهم در ارکستر سلطنتی روسیه تکنوازی میکرد. گئورگِ جوان
در یک خانواده اهل موسیقی بزرگ شد و در نواختن ویولن مهارت پیدا کرد. پدرش، که نام
او نیز گئورگ بود، نماینده یک عمده فروشی در سنت پیترزبورگ بود، که بعداً
به بازار سهام وارد شد. مادرش کاتولیک و پدرش پروتستان بود. در ابتدا او معلم
سرخانه داشت، و بعد به مدرسه ابتدایی رفت. هوای سنت پیترزبورگ در زمستان بسیار
سرد بود، بنابراین خانواده آنها در 1856 به وایزبادن و سپس به فرانکفورت
در آلمان نقل مکان کردند. هرچند کانتور بقیه عمرش را در آلمان سپری کرد، ولی در
نامهای به این نکته اشاره میکند که ’هیچگاه در اینجا احساس آرامش نمیکنم‘، و
همیشه دلتنگ جوانی خودش در روسیه بوده.
کانتور در فرانکفورت به یک مدرسه شبانه روزی رفت. او در 1860 فارغالتحصیل
شد. او را دانشآموز بسیار قابلی توصیف کرده بودند، که مهارت زیادی در ریاضیات،
و خصوصاً در مثلثات داشت. پدر کانتور میخواست پسرش مهندس شود، ولی خودش میخواست
ریاضیات بخواند، و بالاخره با اصرار زیاد پدرش را راضی کرد. او در 1862 در در
دانشگاه پلیتکنیک زوریخ به تحصیل ریاضیات پرداخت. در 1863 پدرش مُرد و برای او
ارثیه قابل توجهای بجا گذاشت، پس از آن او به دانشگاه برلین رفت. در آنجا او در
کلاس استادانی نظیر کرونکر، کومر، و وایراشتراس شرکت میکرد.
در 1866 او تابستان را در گوتینگن سپری کرد، و پس از آن در 1867 پایان نامه خودش تحت
عنوان ’در باب معادلات نامعین درجه دوم‘را ارائه داد، که مبحثی درباره نظریه اعداد
بود.
سپس او بعنوان معلم در یک مدرسه دخترانه استخدام شد، ولی در همان حال روی درجهعالی
خودش کار میکرد. کانتور بعد از گرفتن سِمتی در دانشگاه هاله، رسالهاش
درباره نظریه اعداد را ارائه داد، و درجهعالی خودش را گرفت. ادوارد هاینه (Eduard Heine) که
ریاضیدان برجستهای بود به کانتور پیشنهاد کرد که حوزه خودش را تغییر دهد و به
مسئلهای درباره آنالیز فوریه بپردازد که هنوز حلنشده باقی مانده بود، و آن عبارت
بود از اثبات یکتایی تابعی که به این صورت بیان میشود. دیریله، رودولف لیپشیتس (Rudolf Lipschitz)،
ریمان، و خود هانیه قبلاً تلاش کرده بودند تا این را اثبات کنند، ولی موفق نشدند.
کانتور ظرف مدت یک سال این مسئله را حل کرد. برای مدتی او کارش را بر روی سریهای
مثلثاتی ادامه داد، و تحقیقات او به حوزهای منتهی شد که ما آن را بعنوان پیشنمونه
نظریه مجموعهها میشناسیم. دلیل آن هم این است که بسیاری از خواص سریهای فوریه
بر ویژگیهای ظریفی از تابع نمایش داده شده تکیه دارند (مثلاً ساختار مجموعه نقاطی
که تابع در آن منفصل است). کانتور نمیتوانست در چنین حوزههایی پیشرفتی حاصل کند
مگر اینکه با موضوعهای پیچیدهای مثل مجموعههای نامتناهی اعداد حقیقی روبرو شود.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

سوفیا کووالوسکایا (Sofia Kovalevskaia): تولد: 15 ژانویه 1850،
روسیه. وفات: 10 فوریه 1891، سوئد.
سوفیایِ
جوان از عنفوان کودکی عطش فراوانی برای درک آنچه در پیرامونش میگذشت داشت.
علاقه او به ریاضیات در سن یازده سالگی بروز کرد، و گویا دلیل آن هم کاغذ دیواریهای
اطاقش بود. پدرش، واسیلی، در امپراتوری روسیه سپهبد توپخانه بود، و مادرش یلیزاوتا
از یک خانواده نجیبزاده معروف روسی بود. داستان کاغذدیواری به یک خانه ییلاقی
مربوط میشود که آنها در نزدیکی سنت پیترزبورگ داشتند. آنها هنگامی که میخواستند
به آنجا بروند، دکوراسیون تمام خانه را از نو تغییر دادند، ولی برای اطاقِ کودک به
اندازه کافی کاغذ دیواری نخریده بودند. آنها بجای کاغذ دیواری، از صفحات یک کتاب
درسی قدیمی استفاده کردند. از قضا، این کتابی درباره حساب دیفرانسیل و انتگرال
بود. سوفیا در زندگینامه خودش بنام خاطرات کودکی میگوید ساعتها به
دیوارهای اطاق چشم میدوخت، و سعی میکرد معنی علامتهای پر رمز و رازی که بر روی
صفحات کاغذ چاپ شده بود را بفهمد. او خیلی زود فرمولها را حفظ کرد، ولی بعدها گفت
که ’در آن زمان که به آنها نگاه میکردم نمیتوانستم همه آنها را درک کنم.‘
او قبلاً هم به این گونه خود-آموزیها عادت کرده بود. در آن زمان رسم نبود که
به کودکان خواندن یاد بدهند، ولی سوفیا تشنه خواندن بود. او در سن شش سالگی شکل
الفبا را از روی روزنامهها حفظ کرده بود، و از بزرگترها درباره معنی آنها میپرسید.
او قابلیتهای تازهاش را به پدرش، که شکاک بود، نشان داد. در ابتدا او فکر میکرد
که سوفیا تنها چند جمله را حفظ کرده، ولی بزرودی هوش فراوان دخترش مایه مباهات او
شد.
هنگامی که کاغذدیواریهای اطاق سوفیا موجب برانگیختن علاقه او به ریاضیات شد،
خانواده وی، که از روشنفکران زمان خودشان بودند، کاری نکردند که موجب دلسردی او
شود، هر چند در آن دوره خیلیها ریاضیات را موضوع مناسبی برای یک دختر جوان نمیدیدند.
شرایط دست به هم داد تا او رشته مورد علاقه خودش را دنبال کند. ریاضیات یکی از
موضوعات محبوب پدرش بود، و سوفیا نیز دختر محبوبش بود. پدرِ مادرش، فدور
فدورویچ شوبرت یک نقشه بردار نظامی بود، و پدر او یک ستارهشناس مشهور و عضو
فرهنگستان علوم روسیه بود. بنابراین خون ریاضی در رگهای سوفیا در جریان بود. پدر
نظامی سوفیا، اطمینان یافت که معلمهای سوفیا درسهای پایه، مثل حساب را خوب به
او یاد میدهند. ولی هنگامی که پدرش با اشتیاق نظرش را درباره این موضوع پرسید، در
ابتدا او بدون نشان دادن اشتیاقی جواب داد ’خوب، اینکه حسابان نیست!‘ ولی
وقتی متوجه شد بدون یادگیری این اصول هرگز نمیتواند آن فرمولهای محسور کننده روی
کاغذ دیواریها را درک کند، نهایتاً نظرش عوض شد. بعداً او نه فقط در حسابان استاد
شد، بلکه قدم به پیشرفتهترین تحقیقات ریاضی گذاشت و کشفیاتی را انجام داد که
ریاضیدانان برجسته زمان خودش را شگفت زده کرد. او بر روی معادلات
دیفرانسیل جزئی (partial
differential equations)، مکانیک، و
پراش
نور توسط بلورها کار کرد. انتشارات ریاضی او تنها به ده کتاب محدود میشود، و یکی
از آنها که به زبان سوئدی ترجمه شد، بعداً به زبانهای دیگری نیز برگردانده
شد، ولی کیفیت کتابهای او بسیار بالا بود. او به عمق موضوعات وارد میشد، و کارهایش
اصیل و حاوی زبردستی ماهرانهای بود. ریاضیدان برجسته آمریکایی مارک کس (Mark Kac) از
او بعنوان ’ اولین بانوی بزرگ ریاضیات‘ نام میبرد. بدون تردید او اولین
بانوی دانشمند زمان خودش بود، و فقط چند دهه بعد بود که جهان تحتالشعاع کسی مثل ماری
کوری قرار گرفت.
![]()
سووفیا در سال 1850 در موسکو بدنیا آمد. او خواهر بزرگتری بنام آنا
داشت که بسیار او را دوست داشت، و بعداً صاحب برادری بنام فئودور نیز شد.
عموی او پیوتر واسیلیویچ علاقه زیادی به ریاضیات داشت، و اغلب اوقات، حتی
پیش از اینکه سوفیا بتواند حرفهای او را بطور کامل در کند، با او درباره این
موضوعات صحبت میکرد.
در 1853 هنگامی که سوفیا سه ساله بود، روسیه درگیر جنگهای کریمه شد.
ظاهراً این درگیری به حقوق اقلیتهای مسیحی در سرزمینهای مقدس مربوط بود، ولی
فرانسه و بریتانیا مصمم بودند تا روسیه را از تصرف نواحی امپراتوری رو به زوال
عثمانی باز دارند. در 1856 اتحاد میان فرانسه، بریتانیا، ساردینیا، و عثمانیها،
پس از محاصره سواستُپول، موجب شکست روسها شد. آزادیخواهان به همراه
روستاییان بر علیه دستگاه حالم، که از نظر آنها بطور فزایندهای فاسد و بیکفایت
شده بود، قیام کردند. پاسخ دولت سانسور و سرکوب توسط پلیس مخفی تزاری بود. بسیاری
از نُجبا مالک زمینهای وسیع بودند، ولی کمتر وقتشان را در آنجا سپری میکردند، و
سنتپیترزبورگ و نخبگان سیاسی و اجتماعی آن را ترجیح میداند. حالا احتیاط حکم میکرد
که حتی مالکانی که تمایلات آزادیخواهانه هم داشتند بیشتر وقت خودشان را در روستاها
بگذرانند و به رعایای خودشان توجه بیشتری نشان دهند. بنابراین در 1858 ژنرال
کوروین-کروکووسکی به همسرش گفت که باید به زمینهای روستایی خودشان نقل مکان کنند.
در ابتدا سوفیا و خواهرش آنا را به حال خودشان رها کرده بودند، تا در طبیعت
گردش کنند. ولی پس از اینکه آنها تعدادی توت فرنگی سمی خوردند، و روزها مریض شدند،
پدرشان یک معلم سر خانه لهستانی بنام ایوسف مالِویچ و یک پرستار انگلیسی
بنام مارگاریتا اسمیت را استخدام کرد، که دخترها خیلی از او بدشان میآمد.
مالِویچ به سوفیا دروس ابتدایی را یاد داد که دخترهای جوان باید یاد میگرفتند، از
جمله حساب، ولی عمویش پیتر او را با برخی از رموز ریاضیات پیشرفته آشنا کرد – موضوعاتی مثل تربیع دایره (یعنی ساختن مربعی که مساحت آن به
اندازه یک دایره مفروض باشد، که در واقع با ابزارهای سنتی مثل خطکش و پرگار چنین
کاری غیر ممکن است)، و خطوط مجانب (خطوطی که بطور بینهایت همراه با
یک منحنی امتداد مییابند و بدون اینکه هیچ وقت آن را قطع کنند، به آن نزدیکتر میشوند).
این مفاهیم تخیلات سوفیا را برانگیخت، و باعث شد تا عطش او بیشتر شود.
سرانجام خانم اسمیت استعفا داد و آرامش به خانواده کوروین-کروکووسکی بازگشت.
در 1864 آنا دو داستان برای فئودور داستايفسكي[5] (Fyodor Dostoevsky) و پدرش میخائیل فرستاد، که در نشریه آنها بنام اپوخا
چاپ شد. آنا بعداً مکاتبات مخفیانهای را با فئودور آغاز کرد، که پدرش با آن مخالف
بود ولی پس از اینکه او آرام شد، داستایفسکی به بخشی از حلقه خانوادگی آنها بدل
شد. سوفیا نیز به این حلقه پیوست، و با چهرههای برجسته دیگری آشنا شد. برای مدتی
او مانند دختر بچهها خاطر خواه داستایفسکی شده بود. هنگامی که تئودور به آنا
پیشنهاد ازدواج داد، با اینکه خواهرش درخواست او را رد کرده بود، ولی سوفیا از این
مورد عصبانی بود.
در همین دوران، درحالی که او در اسرار ریاضی کاغذ دیواریهای اطاقش غرق شده
بود، یکی از مسیرهای زندگی او تعیین شد. یکی از همسایگان آنها، بنام نیکولای
تیرتوف، که در آکادامی دریایی سنتپیترز بورگ استاد فیزیک بود، برای سوفیا یک
کتاب درسی درباره فیزیک مقدماتی خرید. او که مثلثات نمیدانست، تلاش کرد موضوع
مورد بحث را با یافتن روشی که بیشتر هندسی بود درک کند (که در واقع استفاده از
کمان یک دایره بود). تیرتوف که از قابلیت او به هیجان آمده بود، سپهبد را تشویق
کرد تا به سوفیا اجازه دهد به مطالعه ریاضیات عالی بپردازد.
![]()
در آن زمان زنان روسی اجازه ورود به دانشگاه را نداشتند، ولی آنها میتوانستند
با یک اجازهنامه کتبی، که از طرف پدر یا شوهر ارائه میشد، در دانشگاههای خارجی
به تحصیل بپردازند. بنابراین سوفیا تصمیم گرفت با شخصیی بنام ولادیمیر
کووالوسکی، که یک دانشجوی جوان دیرینشناسی بود، یک ’ازدواج صوری‘ را انجام
دهد. در آن زمان اینگونه ازدواجها که بدور از روابط واقعی بودند در میان زنان
روسیِ تحصیل کرده عادی محسوب میشد، زیرا به آنها آزادی تحصیل میداد. ولی پدرش میگفت
که او باید دست نگه دارد. بنابراین او تصمیم گرفت تا بعد از یکی از میهمانیهایی
که در خانه آنها برگزار میشد، آنجا را ترک کند، و با گذاشتن یادداشتی گفت که او
بدون داشتن همراهی به خانه ولادیمیر رفته و تا وقتی اجازه ازدواج به او ندهند آنجا
خواهد ماند. پدرش برای حفظ آبرو، در یکی از مهمانیها نامزدی سوفیا و ولادیمیر را
اعلام کرد. قصد سوفیا این بود که پس ازدواج، ولادیمیر را ترک کند و راه خود را
ادامه دهد. ولی ولادیمیر عاشق زن آینده خودش، و محیط اجتماعی او شده بود و نمیخواست
از او جدا شود. آنها زمانی که سوفیا 18 ساله شد، در 1868 ازدواج کردند، و او به
خانم سوفیا کووالوسکایا تغییر نام داد.
مانند بسیاری از جوانان روسی آن زمان، دیدگاههای سیاسی آنها بیشتر هیچگرا (nihilist)
بود. به این معنی که آنها هر مرامی که فاقد پشتیبانی عقلی بود را رد میکردند،
چیزهایی مثل دولت و قانون. ولادیمیر لنین (Vladimir Lenin)، از
نویسنده تندرو دیمیتری پیسارِو نقل قول میکند که ’باید شکست، همه چیز را
بشکنید، بزنید و نابود کنید! هر چیزی که شکسته بیارزش است و حق زندگی ندارد! آنچه
که میماند خوبی است.‘ هنگامی که عروس و داماد به سنت پیترزبورگ رسیدند، آپارتمان
آنها محفلی برای هیچگراها شد.
در 1869 آنها روسیه را ترک کردند، و ابتدا عازم وین شدند. کار چاپ و نشر
ولادیمیر با شکست روبرو شد، و او از دست طلبکاران فرار میکرد؛ هر دو آنها به
دنبال فضای روشنفکرانهتری نیز بودند. ولادیمیر به زمینشناسی و دیرینشناسی علاقه
داشت. بر خلاف انتظار کووالوسکایا، به او اجازه داده شد تا در دانشگاه فیزیک تدریس
کند، ولی بعلت فقدان وجود ریاضیدانان قابل، آنها به هایدلبرگ نقل مکان کردند. در
ابتدا مقامات دانشگاه بدلیل اینکه سوفیا ظاهراً یک بیوه بود او را دَوَل میداند،
و وقتی فهمیدند او ازدواج کرده تعجب کردند، ولی نهایتاً موافقت کردند او بتواند
درسهایی را بردارد که استادان با آن مخالفتی نداشته باشند. بزودی او بیست ساعت در
هفته را صرف درسهایش میکرد، دروسی که توسط ریاضیدانانی چون لئو کونیگزبرگر (Leo Königsberger) و پل دوبوا ریموند (Paul DuBois-Reymond)،
فیزیکدانانی مثل گوستاو کیرشهف (Gustav Kirchhoff) و
فیزیولوژیستهایی نظیر هرمان هلمهولتز تدریس میشد.
او همچنین شیمیدان معروف آن زمان روبرت بونزن را بستوه درآورده بود که
به او و دوستش یولیا لرمونتووا اجازه دهد تا در آزمایشگاهش کار کنند، جایی
که بونزن قسم خورده بود پای هیچ زنی به آنجا باز نخواهد شد، خصوصاً یک زن روسی.
بونزن نزد وایرشتراس گله میکرد که ’این زن مرا مجبور کرده تا از حرفهایم پس بکشم
...‘ و برای تلافی، شایعاتی را درباره کووالوسکایا پخش کرد. ولی در مقابل همکاران
او نظر مثبتی نسبت به همکار مونث خود داشتند، و روزنامهها نیز هر از چندگاهی
مقالاتی را درباره او منتشر میکردند. کووالوسکایا اجازه نداد این مسائل در ذهنش
رخنه کند، و حواسش را بر روی مطالعات خودش متمرکز کرد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

هانری پوانکاره (Henri Poincaré):
تولد: 29 آوریل 1854، فرانسه. وفات: 17 جولای 1912، فرانسه.
ایدههای
ارشمیدس در حمام شکل میگرفت. ولی
این برای پوانکاره درحالی اتفاق میافتاد که سوار بر اتوبوس بود.
هانری پوانکاره یکی از مبتکرترین و اصیلترین
ریاضیدانان دوران خودش بود. او همچنین چندین کتاب پرفروش عامهفهم علمی نوشت که از
متن سخنرانیهایی گرفته شده بودند که او در انجمن فیزیولوژی پاریس ایراد کرده بود.
او به روند تفکر ریاضیدانان، و خصوصاً بر ذهن ناخودآگاه علاقه داشت. او در کتاب علوم
و روش مثالهایی از تجارب خودش را به هم پیوند میزند:
برای مدت دو هفته من در تلاش بودم تا ثابت کنم که هیچ تابعی مثل توابع فوکسی (Fuchsian functions) نمیتواند وجود داشته باشد. من بسیار نادان بودم، زیرا هر روز
یکی دو ساعت جلوی میزم مینشستم، و تعداد زیادی از ترکیبات را بررسی میکردم و در
نهایت به هیچ نتیحهای نمیرسیدم. یک شب برخلاف عادتم، مقدار زیادی قهوه تلخ خورده
بودم و نمیتوانستم بخوابم. آن موقع بود که ایدهها به مغزم هجوم آوردند. احساس میکردم
آنها با هم برخورد میکنند تا اینکه جفتها با هم همبند شوند، و به عبارتی، یک
ترکیب پایدار را تشکیل دهند. تا صبح روز بعد من توانستم وجود یک کلاس از توابع
فوکسی را کشف کنم، همانهایی که از دنبالههای ابرهندسی (hypergeometric) میآیند. تنها کاری که باید انجام میدادم این بود که تنایج را
یادداشت کنم، که فقط چند ساعت طول کشید.
سپس او به جزئیات تجارب خودش میپردازد. لازم است اشاره کنم که لازم نیست شما
کلیه اصطلاحاتی که در پاراگراف زیر آمده را بطور کامل درک کنید. فقط آنها را بعنوان
موضوعات پیشرفته ریاضی تلقی کنید:
من میخواستم این توابع را بعنوان خارج قسمت دو دونباله بیان کنم. این ایده
کاملاً آگاهانه و عمدی بود، راهنمای من تشابهی بود که در توابع بیضوی وجود داشت.
من از خودم پرسیدم که در صورتی که چنین دنبالههایی وجود دارند، آنها باید چه
ویژگیهایی را دارا باشند، و بدون هیچ مشکلی موفق شدم این سریها، که اسم آنها را تتا-فوسکی (theta-Fuchsian) گذاشتم، بسازم. در همین زمان من شهری که در آن زندگی میکردم
(کان) را ترک کردم و به یک سفر اکتشافی رفتم. این سفر باعث شد من کارهای ریاضی خود
را فراموش کنم. به شهر کوتانس که رسیدیم سوار اتوبوسی شدم که به جای دیگری بروم.
هنگامی که پا در رکاب اتوبوس گذاشتم ایدهها به سراغم آمدند، همه چیز از قبل هموار
شده بود، و تبدیلاتی که من برای تعریف توابع فوسکی از آنها استفاده کرده بودم با
آنهایی که در هندسههای نا-اقلیدسی بود یکسان بودند. من این ایده را بررسی نکردم،
زیرا وقت زیادی نداشتم، همانطور که در اتوبوس نشسته بودم وارد گفتگویی شدم که از
قبل شروع شده بود، ولی نسبت به این ایده کاملاً اطمینان داشتم. در بازگشتم
به کان، برای اینکه خیالم راحت شود نتایج را بررسی کردم.
این داستان با دو مورد دیگر از الهامات ناگهانی ادامه مییابد.
پوانکاره با ژرفاندیشی در کشفیات ریاضی خودش، سه مرحله را در آنها تشخیص میدهد:
دوره آمادهسازی، تکوین، و نهایتاً الهام. بعبارتی، کار را چنان آگاهانه انجام
دهید که در مسئله فرو روید و آنجا گیر کنید. صبر کنید تا ناخودآگاه شما کارش را
انجام دهد، و چراغ کوچک ذهنتان روشن شود، این همان لحظهِ معروفِ ’یافتم!‘ است.
این هنوز هم یکی از بهترین بصیرتهایی است که ما برای عملکرد ذهنهای بزرگ
ریاضی در اختیار داریم.
![]()
هانری پوانکاره در شهر نانسی فرانسه متولد شد. پدرش لئون در دانشگاه
نانسی استاد پزشکی بود، و مادرش اوژنی نام داشت. پسر عموی او ریموند
پوانکاره نخست وزیر فرانسه شد، و بعداً در طول جنگ جهانی اول بعنوان رئیس
جمهور فرانسه برگزیده شد. زمانی که هانری بچه بود به دیفتری مبتلاء شد، و تا وقتی
که خوب نشد مادرش در خانه به او درس میداد. او در نانسی یازده سال به مدرسه رفت و
کلیه درسهایش عالی، و ریاضیاتش بسیار عالی بود، طوری که برنده جایزه ملی شد. معلمش
به او لقب ’غول ریاضیات‘ را داده بود. او حافظهای بسیار قوی داشت و میتوانست
اشکال پیچیده سه-بعدی را در ذهنش مجسم کند. این میتوانست بینایی ضعیف او، که
بسختی میتوانست تخته سیاه را ببیند، چه رسد روی آن چیزی بنویسد، را جبران کند.
در 1870 جنگ روسیه-فرانسه در اوج خودش بود، و پوانکاره به همراه پدرش در رسته
بهیاران خدمت میکرد. جنگ در 1871 تمام شد، و او در 1873 در کنکور دانشکده پلیتکنیک
پاریس شرکت کرد، و در 1875 فارغالتحصیل شد. سپس به مدرسه عالی معدن رفت، تا معدنشناسی
و مهندسی و همچنین ریاضیات پیشرفته بخواند. او در حومه وسول بازرس
معدن شد، و این مصادف با تحقیقات حادثه ریزش معدن ماگنی بود که در طی آن
هجده نفر کشته شدند. او همچنین زیر نظر هرمیت به گرفتن مدرک دکترای خودش در
زمینه معادلات تفاضلی مشغول بود. این معادلات مشابه معادلات دیفرانسیل هستند، با
این تفاوت که در اینها تغییرات بجای اینکه پیوسته باشند گسسته هستند. او به کاربرد
بالقوه این معادلات در مدلسازی بسیاری از اجسام متحرک که تحت جاذبه حرکت میکنند،
مثل اجرام منظومه شمسی، پی برد. البته بکارگیری این روشها به محاسبات سنگینی نیاز
داشت که برای انجام آنها باید کامپیوتر اختراع میشد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

داوید هیلبرت (David Hilbert): تولد: 23 ژانویه 1862،
پروسیا. وفات: 14 فوریه 1943، آلمان.
یک
استاد ریاضی شصت و هشت ساله مجبور شد بازنشسته شود. هنگامی که در 1930 داوید هیلبرت این
مرحله مهم از زندگی خودش را پشت سر گذاشت، مراسم زیادی برای گرامیداشت دوران حرفهای
او برگزار شد. او به مناسبت اولین کشف بزرگ خودش، یعنی وجود یک متناهی برای ناواردها (invariants) یک
سخنرانی ارائه داد. هنگامی که همسرش به او گفت ’ فکر خوبی است که میخواهند یک خیابان
را بنام تو نامگذاری کنند!‘ هیلبرت در جواب گفت، ’فکر چندان خوبی نیست، ولی اگر
بشود خوب است، کلاین باید منتظر میماند تا بعد از مرگش اینکار را برای او
انجام دهند.‘
بهترین اینها عطای شهروندی افتخاری کوینسبرگ (Königsberg)
بود. کوینسبرگ شهری است که هیلبرت در نزدیکی آن بدنیا آمده بود. اهدای این شهروندی
قرار بود در مراسمی با حضور دانشمندان و فیزیکدانان آلمانی صورت گیرد، و هیلبرت
باید درآنجا سخنرانی میکرد. او تصمیم گرفت که چیزهایی را بگوید که بطور گستردهای
قابل قبول باشند، و بدیل اینکه فیلسوف شهیر آلمانی امانوئل کانت (Immanuel Kant) در
همین شهر متولد شده بود، بد نبود که سخنرانی او جنبههای فلسفی نیز داشته باشد،
همچنین باید حاوی یک جمعبندی از کارهای خود او نیز باشد. عنوانی که او برای
سخنرانی خود انتخاب کرد ’علوم طبیعی و منطق‘ بود. هیلبرت در چنین موضوعاتی فعال
بود، و غالباً در روزهای شنبه یک سری سخنرانیها را برای عموم مردم در دانشگاه
ارائه میداد، موضوعاتی مثل نسبیت، بینهایت، اصول ریاضیات، ... و تمام تلاشش را
میکرد که آنها برای همه علاقهمندان قابل فهم باشد. حال او باید تمام سعی خود را
بکار میگرفت که همه آنها را در قالب یک سخنرانی جمعبندی کند.
او سخنان خودش را اینطور شروع کرد: ’ والاترین وظیفه ما درک طبیعت و حیات
است،‘ و سپس به مقایسه و تباین دو روشِ درک ما از جهان پرداخت، که از نظر او یکی
تفکر و دیگری مشاهده بود. این دو از طریق قوانین طبیعت با یکدیگر پیوند دارند،
قوانینی که باید از راه مشاهده استنتاج شده و توسط منطقِ محض توسعه یابند.
این دیدگاهی بود که کانت داشت، و طعنهآمیز این بود که هیلبرت خیلی طرفدار کانت
نبود. البته حالا موقع مناسبی برای مخالفت با کانت نبود، و در این موردِ خاص نیز
اختلافی وجود نداشت، ولی هیلبرت درباره یک مورد نمیتوانست جلوی خودش را بگیرد، و
آن چیزی بود که کانت بر اهمیت آن خیلی تکیه کرده بود و فهمِ پیشینی (a priori)
نام دارد، یعنی درکی که از راه تجارب فکری حاصل نمیشود. هندسه نمونه خوبی از این
است، مثلاً آنطور که کانت استدلال میکرد، هیچ دلیل خاصی نبود که فرض کنیم فضا
لزوماً اقلیدسی است. ولی اگر ویژگیهای انسانانگارانه را برداریم، مفهومِ پیشینی
صحیح باقی میماند، به عبارتی، تمامیت ریاضیات. او در سخنان خودش اینطور گفت : ’
تا آنجا که به درک ذهنی ما و غلبه بر طبیعت مربوط است، کُل تمدن فعلی ما بر پایه
ریاضیات قرار دارد!‘ و دلیل اینکه از ریاضیاتِ محض انتقاد میشد این است که کاربرد
عملی ندارد. او سخنانش را با دفاع از این حوزه پایان داد و گفت : ’نظریه اعدادِ
محض بخشی از ریاضیات است که تا به امروز هیچ کاربردی برای آن پیدا نشده ...
ولی یگانه هدفِ تمامیِ علم درخشش ذهن انسان است!‘
این سخنرانی به قدری با استقبال روبرو شد که هیلبرت قانع شد آن را در رادیو
محلی نیز ارائه دهد، که نسخههای ضبط شده آن هنوز باقی است. او تاکید کرد که
مسائلی که قبلاً غیر ممکن تصور میشد – مثل یافتن ترکیبات
شیمیایی یک ستاره – افقهای جدیدی را در مقابل ما قرار داده. او گفت ’چیزی بنام مسئله غیرقابل حل
وجود ندارد،‘ و آخرین جملهِ سخنرانی او اینطور تمام شد ’ما باید بدانیم، و
خواهیم دانست.‘ سپس در حینی که مسئول ضبط صدا نوار را متوقف میکند، هیلبرت میخندد.
در آن زمان هیلبرت درگیر برنامه سنگینی بود که هدف آن پایهگذاری تمامِ
ریاضیات بر بنیانهای منطق بود، و سخنان او بیانگر این اعتقاد بود که این برنامه
به ثمر خواهد نشست. البته از قبل هم پیشرفتهای زیادی در اینباره حاصل شده بود.
تنها چیزی که باقی مانده بود چند مورد ظریف بود که باید به آنها رسیدگی میشد. اگر
آنها تهذیب میشدند، هیلبرت نه فقط برای کل ریاضیات یک پایه منطقی داشت، بلکه قادر
بود اثبات کند که اصول موضوعه او از لحاظ منطقی سازگار هم هستند.
البته کارها آنطور که او انتظار داشت پیش نرفت.
![]()
هیلبرت از خانوادهای میآمد که همه در کار حقوق بودند. پدر بزرگش یک قاضی و
عضو مشاوران سلطنتی بود، پدرش اوتو یک قاضی محلی بود. مادرش ماریا
دختر یک بازرگان اهل کوئینسبرگ بود. مادرش به فلسفه، ستارهشناسی، و اعداد اول
علاقه داشت، و بنظر میرسد این علایق را به پسرش نیز منتقل کرده بود. هنگامی که
داوید شش ساله بود، صاحب خواهری بنام السی شد. تا وقتی داوید در سن هشت
سالگی به مدرسه نرفته بود، مادرش در خانه به او درس میداد. در مدرسه به او ادبیات
کلاسیک و مختصری ریاضیات آموزش میدادند و خبری هم از علوم نبود. در آن زمان دروس
حفظ کردنی مد روز بود، و هیلبرت هم به چیزهایی که فاقد ساختار بودند و نیاز به حفظ
کردن داشتند حساسیت داشت. او خودش را بعنوان یک دانشآموز ’کودن و ابله‘ توصیف میکرد.
یک درس در این میان استثنا بود. گزارشهایی که از مدرسه او بجا مانده اینطور میگوید: ’او همیشه نسبت به دروس ریاضی علاقه و فهم بالایی را نشان میدهد:
او در تمام مواردی که در مدرسه آموزش داده شده مهارت زیادی را کسب کرده و قادر است
با نبوغ و خاطر جمعی آنها را بکار گیرد.‘
در 1880 هیلبرت به دانشگاه کوئینسبرگ وارد شد و از آنجا در ریاضیات فارغالتحصیل
شد. او در هایدلبرگ تحت نظر لاتساروس فوکس (Lazarus Fuchs) یک سری
دروس را اختیار کرد، و در بازگشت به کوئینسبرگ تحت نظر هاینریش وبر، فردیناند
لیندمان، و آدولف هورویتز به مطاله پرداخت. او با افرادی مثل هورویتز و هرمان مینوکفسکی، که همکلاس خودش بود،
دوستی نزدیکی داشت. هیلبرت در طول عمرش ارتباط خودش با مینوکفسکی را حفظ کرد.
لیندمان، که بخاطر اثبات غیر جبری بودن عدد π مشهور است، استاد راهنمای هیلبرت شد. او به هیلبرت پیشنهاد داد تا
بر روی نظریه تغییرناپذیرها (invariant
theory) کار کند، موضوعی که توسط بول مطرح شد و کسانی مثل کیلی، سیلوستر، و پل گوردان آن را گسترش دادند. روشهای
آنها بر اساس محاسبات قرار داشت، و مهارت هیلبرت در این محاسباتِ سنگین، دوستش
مینوکفسکی را تحت تاثیر قرار داد. در 1885 هیلبرت پس از ارائه یک سخنرانی عمومی درباره
فیزیک و فلسفه، دکترای خودش را دریافت کرد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

امی نوتر (Emmy Noether): تولد: 23 مارس 1882،
آلمان. وفات: 14 فوریه 1935، آمریکا.
در سال
1913 امی نوتر، که ریاضیدان زن مشهوری
بود، برای ارائه یک سری درسها در وین به سر میبرد، و به دیدار فرانز مرتنز (Franz Mertens) رفته
بود. مرتنز ریاضیدانی بود که در بسیاری از حوزههای ریاضی کار کرده بود ولی بیشتر
بخاطر سهمی که در نظریه اعداد دارد معروف است. بعدها یکی از نوههای مرتنز خاطرهای
که از این دیدار داشت را اینطور تعریف میکند:
هر چند او یک زن بود، ولی با لباسِ تمام سیاهی که به تن کرده، و تا قوزک پایش
کشیده شده بود، با کتش و کلاه سیاه مردانهای که روی موهای کوتاهش گذاشته بود،
شبیه کشیشان یک کلیسای روستایی بنظر میرسید ... و با کیسهای که بدوش خودش
انداخته بود و شبیه ماموران خط آهن دوران ویکتوریا بود، قیافه بسیار عجیبی داشت.
دو سال بعد، این زنِ بیتکلف مسئول یکی از بزرگترین کشفیات در فیزیک ریاضی شد،
یعنی پیوند اساسی که میان تقارنها و قوانین پایستگی وجود دارد. از آن زمان به
بعد، تقارنِ قوانینِ جهان نقش مهمی در فیزیک پیدا کرد. امروزه آنها پایه ’مدلِ
استاندارد‘ ذرات زیراتمی در نظریه کوانتوم هستند، که تقریباً غیرممکن است بدون
استفاده از تقارن بتوان آنها را توضیح داد.
نوتر یکی از شخصیتهای پیشرو در توسعه جبر مجرد (astract algebra) بود. در
جبر مجرد، محاسبات با بسیاری از گونههای مختلف اعداد یا فرمولها بشکل قوانین
جبری که این سیستمها از آن پیروی میکنند، سازماندهی میشود. شاید بیش از هر
ریاضیدان دیگری کسی که بیشترین سهم در مزبندی میان جبر اواخر قرن نوزدهم، که بیشتر
بر روی ساختارهای خاص و فرمولها تکیه میکرد، و جبر مدرن قرن بیستم، که از دهه
1920 شروع میشد و بر عمومیت، تجرید، و مفاهیم فکری تکیه داشت، کسی نبود جز آن زن
عجیبی که نوه مرتنز او را توصیف کرده بود. نوتر محرک اصلی جنبش بورباکی (Bourbakiste) در
ریاضیات بود. بورباکی نام مستعار گروهی ار ریاضیدانانِ جوانِ عمدتاً فرانسوی بود
که هدفشان صریح و کلی کردن ریاضیات بود. از نظر خیلیها، حاصل کار آنها کلی کردن بیش
از حد ریاضیات بود.
![]()
امی نوتر در یک خانواده یهودی در شهر ارلانگن استان باواریا
متولد شد. پدرش مارکس ریاضیدان برجستهای بود که بر روی هندسه جبری و نظریه
توابع جبری کار کرده بود. او در مقایسه با ریاضیدانان هم دوره خودش بسیار با
استعداد بود. او خانواده متمولی داشت. بدون تردید سابقه این خانواده بر گرایشهای
امی نسبت به زندگی و ریاضیات تاثیر داشت. او ابتدا میخواست معلم شود، و مدارک
لازم جهت تدریس زبانهای فرانسه و انگلیسی را کسب کرد. ولی جای تعجب نداشت که بالاخره
تحت تاثیر پدرش با ریاضیات عالی آشنا شد و در دانشگاه ارلانگن شروع به تحصیل در
این رشته کرد.
دو سال پیش از این شورای دانشگاه اعلان کرده بود که آموزش کلاسهای مختلط
متشکل از زنان و مردان ’باعث میشود کلیه مراتب دانشگاهی برهم بخورد!‘، و جالب
اینکه از میان 986 دانشجو تنها دو نفر آنها زن بودند. به امی اجازه داده شد تا
بصورت مستمع آزاد در کلاسها حاضر شود، ولی حق نداشت بطور کامل شرکت کند، و برای
حضور خودش در سر کلاسها باید بطور مجزا از استادان اجازه میگرفت. ولی در 1904
قوانین تغییر کرد، و به زنان اجازه داده شد تا همپای مردان در دانشگاهها ثبتنام
کنند. نوتر نیز در 1904 همین کار را کرد، و به دانشگاه گوس، یعنی گوتینگن، رفت تا
دکترایش را در زمینه نظریه تغییرناپذیرها زیر نظر گوردان اخذ کند. محاسباتی
که در رساله دکترایش ارائه کرده بود بطور خارقالعادهای پیچیده بودند، و شامل
فهرستی از 331 همگرد (covariant) درجه چهارم با سه متغیر بود. گورانِ خستگی ناپذیر، خودش چهل سال
قبل از چنین محاسبات سنگینی دست برداشته بود. روشهای نوتر قدیمی بودند، و توجه
زیادی به ابداعاتی که هیلبرت در این زمینه کرده بود نداشتند. او در 1907 دکترای
خودش را با درجه ممتاز از دانشگاه گوتینگن گرفت.
اگر نوتر یک مرد بود، قاعدتاً مرحله بعدی زندگی او این بود که در یک دانشگاه
سِمتی دائم را برای خودش بگیرد. ولی زنان حق نداشتند درجهعالی بگیرند، بنابراین
او به مدت هفت سال بدون حقوق در دانشگاه ارلانگن کار کرد. او کمک دست پدرش، که در
آن زمان معلولیت پیدا کرده بود، شد و تحقیقات خودش را نیز ادامه داد. در گفتگوهایی
که نورتر با ارنست فیشر داشت، فیشر توجه او را به سمت روشهای جدید هیلبرت جلب کرد
و به او توصیه کرد از آنها استفاده کند. این تجربه سازندهای برای نورتر بود، و او
را بیشتر به سمت روشهای مجرد سوق داد. او با کمال میل این توصیه را پذیرفت، چیزی
که بخوبی تاثیر آن در باقی دوران حرفهای او آشکار بود.
ریاضیات کمکم داشت برای زنان گشوده میشد، و نورتر در خیلی از انجمنهای مهم
ریاضی پذیرفته شد. همین بود که به دیدار او از وین و ملاقات با مرتنز و نوه او
منجر شد. در دانشگاه ارلانگن او استاد مشاور دو دانشجوی دکترا بود، که بطور رسمی
تحت نظر پدرش قرار داشتند. سپس هیلبرت و کلاین او را به گوتینگن، که در آن زمان
بخاطر مطالعات ریاضی در سطح جهان معروف بود، دعوت کردند. سال 1915 بود و هیلبرت با
الهام از نسبیتِ عامِ اینشتین به سراغ فیزیک ریاضی رفته بود. نسبیت بر پایه
ریاضیاتِ تغییرناپذیرها قرار داشت، هر چند تغییرناپذیرها در نسبیت عام بیشتر جنبه
تحلیلی داشتند تا جنبه جبری، یعنی همان چیزی که گوردان، هیلبرت، و نورتر بر روی آن
کار کرده بودند. اینجا تغییرناپذیرهای دیفرانسیل (differential invariants) مطرح بودند، که شامل مفاهیم اساسی فیزیکی مثل انحنای فضا بود.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

سرینیواسا رامانوجان (Srinivasa Ramanujan)،:
تولد: 22 دسامبر 1887، هند. وفات: 26 آوریل 1920، هند.
ژانویه
1913 بود. ترکیه درگیر جنگ بالکان
بود و اروپا هرچه بیشتر بسوی کشمکشهای عمیقتر میرفت. گادفری هاردی (Godfrey Hardy) که
در دانشگاه کمبریج استاد ریاضی بود، از جنگ نفرت داشت، و به حوزهای که در آن کار
میکرد، یعنی ریاضیاتِ محض، بسیار افتخار مینمود، زیرا به تصور خودش هیچ کاربرد
نظامی و جنگی نداشت.
در بیرون به آرامی برف میبارید و دانشجویان دوره کارشناسی به تندی در حیاط
حرکت میکردند. ولی در اطاق هاردی آتش دلپذیری روشن بود که سرما را رام میکرد.
روی میز نامههای امروز قرار داشت که باید باز میشد. او به نامهها نگاهی انداخت.
یکی از آنها بدلیل تمبر غیرعادی که داشت نظر او را به خودش جلب کرد. آدرسی که روی
پاکت نوشته شده بود این بود: هند، مَدرَس، 16 ژانویه 1913. هاردی سر پاکت را گشود،
و چند ورقه کاغذ کاهی را در آن دید. به آن کاغذها نامهای ضمیمه شده بود که اینطور
شروع میشد:
آقای عزیز،
اجازه میخواهم خودم را اینطور معرفی کنم که کارمند بخش حسابداری در پورت
تراست مَدرَس هستم، با حقوق سالیانهام 20 پوند در سال. حالا 23 سال دارم. هیچ
تحصیلات دانشگاهی نداشتهام ... پس از فارق شدن از مدرسه اوقات فراقت خودم را صرف
ریاضیات کردهام ... و مسیر جدیدی را برای خودم برگزیدهام.
هاردی پیش خودش فکر کرد ’خدای من، باز هم یک خُل دیگه، احتمالاً فکر کرده که
توانسته مسئله تربیع دایره را حل کند.‘ نزدیک بود هاردی نامه را به سطل زباله
بیندازد، ولی کاغذهایی که همراه نامه بود و بر روی آن علامتهای ریاضی نوشته شده
بود توجه او را جلب کرد. آنها فرمولهای عجیبی بودند، که برخی از آنها برای هاردی
آشنا، و برخی هم غیر معمول بود.
اگر نویسنده نامه آدم خُلی باشد، حداقل شاید قضیه عجیبی را هم اثبات کرده.
هاردی در ادامه نامه چنین خواند:
به تازگی من یکی از کتابهای شما را تحت عنوان ’مراتب بینهایت‘ دیدم که در آن
عبارتی آمده بود که میگفت هنوز هیچ فرمولی دقیقی پیدا نشده تا توسط آن تعداد
اعداد اول کوچکتر از یک عدد مفروض معلوم شود. من برای این قضیه فرمولی را یافتهام
که میتواند تقریب خیلی خوبی از نتیجه واقعی بدست دهد، و خطای آن نیز قابل چشمپوشی
است.
هاردی فکر کرد، خدای من او قضیه اعداد اول را از نو کشف کرده.
از شما درخواست میکنم نگاهی به کاغذهای ضمیمه این نامه بیاندازید. بسیار مایل
هستم تا در صورتی که شما قضایای مرا باارزش دیدید، آنها را چاپ کنید. چون بیتجربه
هستم هر راهنمایی که شما بفرمایید آن را قدر مینهم. از اینکه مصدع اوقات شما شدم
پوزش میطلبم.
ارادتمند همیشگی شما،
س. رامانوجان
هاردی باز هم باخودش فکر کرد که این یک آدم خُل معمولی نیست. آدمهای
خل معمولی، طلبکارتر و مغرورتر از این حرفها هستند. او نامه را به کناری
گذاشت و شروع به خواندن کاغذهای ضمیمه کرد. نیم ساعت گذشته بود و او با حالت عجیبی
که صورتش داشت هنوز بر روی صندلی نشسته بود. با خودش فکر کرد، چقدر عجیب است.
هاردی خیلی کنجکاو شده بود، ولی وقت کلاس آنالیز مقدماتی او فرا رسیده بود،
بنابراین ردای استادیِ گچ آلود خودش را پوشید و در اطاق را پشت سرش بست تا به سر
کلاس برود.
آن شب هاردی بر سر میز شام در مورد آن نامه عجیب با همه همکاران خودش که به
چنین چیزهایی اهمیت میدادند صحبت کرد، خصوصاً با دوستش جان لیتلوود (John Littlewood.). لیتلوود مایل بود
ساعتی را به موضوعی که ذهن دوستش را مشغول کرده بود بپردازد، و اطاق پذیرایی هم
خالی بود. همانطور که وارد اطاق میشدند، هاردی که کاغذی را در دست داشت گفت ’این
مرد یا خیلی خُل است یا واقعاَ یک نابغه.‘
یک ساعت بعد هاردی و لیتل وود به وحدت رأي رسیدند. او نابغه بود.
![]()
امیدوارم از اینکه این واقایع را بصورت مبالغه آمیزی بیان کردم مرا ببخشید. من
پیش خودم افکار هاردی را بازگو کردم، ولی اسناد بجا مانده نشان میدهد که آنچه در
ذهن او اتفاق افتاده شباهت زیادی به این داشته باشد.
نویسنده نامه، یعنی سرینیواسا رامانوجان، در سال 1887 در یک
خانواده برهمن متولد شد. پدرش در یک مغازه ساری[6]
فروشی فروشنده بود، و مادرش فرزند یک نگهبان امنیتی بود. او در خانه مادربزرگش در
شهری در استان جنوبی تامیل نادوِ هند، بنام ِارود بدنیا آمد. او در
شهر کومباکنام که پدرش در آنجا کار میکرد بزرگ شد. ولی در آن زمان رسم بود
که زنان علاوه بر خانه شوهرشان، اوقاتی را نیز در خانه والدین خود سپری کنند،
بنابراین مادرش غالباً او را به خانه پدرش که در نزدیکی شهر مَدرَس قرار داشت و با
آنجا 400 کیلومتر فاصله داشت میبرد. خانواده آنها فقیر و خانه آنها کوچک بود. هر
چند رامانوجان خیلی یک دنده بود، ولی روی هم رفته در کودکی زندگی شادی را داشت. او
تا سه سالگی کلمهای به زبان نمیآورد و مادرش میترسید که او لال باشد. پنج ساله
که شد معلمش را دوست نداشت و نمیخواست به مدرسه برود. او ترجیح میداد درباره
چیزهایی که دوست دارد فکر کند، و سئوالات سختی، مثل ’ابرها از یکدیگر چقدر فاصله
دارند؟‘ را میپرسد.
استعداد ریاضی رامانوجان خیلی زود بر ملاء شد، و در سن 11 سالگی از دو دانشجو
که در خانه آنها سکنی گزیده بودند سبقت گرفت. او چگونگی حل معادلات درجه سه را
یادگرفت و میتوانست ارقام اعداد π و
e را به تعداد
زیادی از حفظ بیان کند. یک سال بعد او یک کتاب پیشرفته را قرض گرفت و بدون هیچ
مشکلی کاملاً بر آن مسلط شد. هنگامی که 13 ساله بود با اشتیاق فراوانی کتاب مثلثات
سیندی لونی را خواند که در آن مطالبی درباره بسط بینهایتِ دنبالههای
سینوس و کسینوس آمده بود، و خودش نتایج جدیدی را استنتاج کرد. توانایی او در
ریاضیات باعث شد در مدرسه برنده جوایز فراوانی شود، و در 1904 مدیر مدرسه گفت که
باید به او نمراتی فرای آنچه ممکن است داده شود.
در سن 15 سالگی اتفاقی افتاد که زندگی او را تغییر داد، ولی در آن زمان چیز
مهمی بنظر نمیرسید. او از کتابخانه دانشگاه دولتی نسخهای از کتاب ’خلاصهای
از نتایج مقدماتی در ریاضیات محض‘ نوشته جورج کار (George carr) را
امانت گرفت. البته اینجا منظور از ’خلاصهای از نتایج‘ مهمترین نتایج بود.
تعداد صفحات این کتاب از هزار صفحه بیشتر بود، و حدود پنج هزار قضیه در آن فهرست
شده بود، که همه بدون اثبات آمده بودند. جورج کار کتابش را بر اساس مسائلی
که برای دانشجویان خودش طرح میکرد نوشت. رامانوجان نیز برای خودش یک مسئله طرح
کرد، و آن این بود که کلیه فرمولهای کتاب مذکور را بررسی کند. او هیچ کمک یا کتاب
دیگری در دست نداشت. او بطور کارآمدی برای خودش یک پروژه تحقیقاتی تعیین کرد که
شامل پنجهزار موضوع جداگانه بود. او که بضاعت خرید کاغذ نداشت، محاسبات خودش را
بر روی لوحهای سنگی انجام میداد و نتایج آنها را بر روی دفترچههایی یادداشت میکرد
که تا آخر عمرش آنها را نگه داشته بود.
در سال 1908 مادر رامانوجان، که کومالاتامال نام داشت، تصمیم
گرفت برای پسر بیست ساله خودش زنی را انتخاب کند. او برای اینکار دختر یکی
از اقوام خودش بنام جاناکی را برگزید که در 100 کیلومتری آنها زندگی میکردند.
جاناکی 9 ساله بود. در جامعهای که بر اساس ازدواجهای از پیش تعیین شده و
عروسانِ کم سن و سال بنا شده بود، اختلاف سنی آنها مانع مهمی نبود. اینطور که
پیداست رامانوجان یک جوان بسیار معمولی بود؛ یک جوان کاهل، بیکار، بیپول، و بدون
هیچ آیندهای. جاناکی یکی از پنج دختر خانواده خودش بود که تقریباً همه چیزشان را
از دست داده بودند، و والدین او راضی بودند که او را به عقد کسی در بیاورند که با
او خوب رفتار کند. همین برای مادر رامانوجان کافی بود. ولی پدر رامانوجان وقتی این
را شنید عصبانی شد. از نظر او پسرش میتوانست انتخابهای بهتری داشته باشد. او
بیشتر از این ناراحت بود که چرا همسرش در این مورد با او مشورت نکرده. به هر حال
او ناراحتی خودش را با امتناع از رفتن به عروسی اعلام کرد.
روز عروسی فرا رسید و هیچ اثری از داماد یا خانواده او دیده نمیشد. پدر عروس،
که رانگاسوامی نام داشت، به همه اعلام کرد که اگر سر و کله رامانوجان
بزودی پیدا نشود او فوراً جانانکی را به کس دیگری شوهر میدهد. سر انجام چند ساعت
بعد قطار از راه رسید و رامانوجان و مادرش (منهای پدر) با یک ارابه گاوی به دهکده
وارد شدند. مادر رامانوجان فوراً جواب رانگاسوامی را داد و بطور علنی گفت یک پدر
فقیر با پنج دختر نباید چنین پیشنهادی را رد کند.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

کورت فردریش گودل (Kurt Gödel):
تولد: 28 آوریل 1906، اتریش. وفات: 14 ژانویه 1978، آمریکا.
در
تصویر کلیشهای که از ریاضیدانان ارائه میشود، گذشته از اینکه همه آنها مذکر و سالخوردهاند،
این است که آنها کمی عجیب، قطعاً مُنفک از جهان دنیوی، معمولاً غیرعادی، و برخی
اوقات هم کلاً دیوانه هستند.
گذشته از اینکه بیشتر ریاضیدانان مذکر هستند، ما در این کتاب دیدهایم که چنین
تصویری در مورد بیشتر ریاضیدانان صدق نمیکند، و حتی این تصویر در طول چند دهه
گذشته بکلی تغییر کرده. البته درست است که ریاضیدانان ممکن است در دوران سالخوردگی
هم کار کنند، ولی چه کسی اینکار را نمیکند؟ تنها چیزی که مانع از کار کردن آنها
میشود این است که مانند گالوا جوانمرگ شوند. به دنبال افزایش سن، اعتبار و
مسئولیت نیز افزایش مییابد، بنابراین محتملاً سالاخوردگان در میان بقیه شاخصترند.
هنگامی که ذهن ریاضیدانان بر روی تحقیقاتشان متمرکز میشود، بنظر میرسد که
آنها از این جهان منفک شدهاند، ولی همانطور که یکی از دوستان زیستشناس من همیشه
میگفت، آنها پریشان حواس نیستند، بلکه حواس آنها در جای دیگری مشغول است. اگر
شما بخواهید یک مسئله دشوار ریاضی را حل کنید، ذهن شما باید متمرکز باشد. برخی از
ریاضیدانان در منفک شدن از جهان تا حدی افراط میکنند که حالت آنها عجیب بنظر میرسد.
شاید واضحترین نمونه از چنین ریاضیدانانی پُل اردوش (Paul Erdős) باشد، که هیچ
وقت یک منصب دانشگاهی نگرفت و همیشه هم خانه بدوش بود. او از یک دانشگاه به
دانشگاه دیگر در سفر بود، شبها را بر روی کاناپه، یا در اطاق مهمان دوستانش سپری
میکرد. با اینحال او بیش از 1500 مقاله تحقیقاتی نوشت و با بیش از 500 ریاضیدان
مختلف همکاری داشت، و از این نظر بیهمتا بود.
اما در مورد دیوانه بودن: برخی از آنها دیوانه میشوند، به عبارتی، در مرحلهای
از زندگی خودشان به بیماریهای ذهنی دچار میشوند. کانتور از افسردگی جدی رنج میبرد.
جان
نَش (John Nash)، که موضوع فیلم ’یک ذهن زیبا‘ بود، در 1994 برنده جایزه نوبل
اقتصاد شد، ولی با اینحال سالها از شرایطی رنج میبرد که بعنوان پارانویای
اسکیزوفرنیک از آن نام میبرند، و از شوکدرمانی استفاده میکرد. او با اراده
راسخی که داشت و تشخیص دورههای بیماری، به آنها اجازه بروز نداد و توانست خودش را
درمان کند.
کورت گودل مطمئناً به دسته ریاضیدانان عجیب
تعلق داشت، و زمانی از آن هم فراتر رفت. در آن زمان منطق ریاضی جزء حوزههای اصلی
ریاضیات محسوب نمیشد، ولی او این رشته را برای مطالعات خودش انتخاب کرد، و
از این نظر میتوان او را درمیان همکارانش به کسانی تشبیه کرد که منفک از این جهان
بودند. در عوض کشفیات او در آن حوزه، تفکر ما درباره مبانی منطق و ریاضیات، و
چگونگی تعامل آنها با هم، را بکلی تغییر داد. ایدههای او بطور درخشانی اصیل و
بطور برجستهای ژرف بودند.
علاقه او به منطق هنگامی شروع شد که در سال 1933 آدولف هیتلر در آلمان به قدرت
رسید. الهام بخش او در این زمینه سمینارهای فیلسوف آلمانی موریتس شلیک (Moritz Schlick)
بود، که مؤسس پوزیتیویسم و حلقه وین بود. شلیک در 1936 توسط، یوهان نلبوک،
که یکی از دانشجویان سابقش بود ترور شد. پیش از این، بسیاری از اعضای حلقه وین
بدلیل ترس از آزارهای ضد-یهودی از آلمان گریخته بودند، ولی شلیک که در اتریش بود
در دانشگاه وین مانده بود. هنگامی که او از پلهها بالا میرفت تا سر کلاس برود،
نلبوک با یک تپانچه وی را کشت. او به قتل اعتراف کرد، ولی از جلسه دادگاه برای
بیان دیدگاههای سیاسی خودش استفاده کرد. او شلیک را به اشاعه دیدگاههای ضد
متافیزیکی متهم کرد. برخی هم عقیده دارند که انگیزه نلبوک برای این قتل احساساتش
به دانشجوی دیگری بنام سیلویا بروویکا بوده. او در خیالات پارانوید (کجپندارانه)
خودش فکر میکرده که شلیک رقیب او در این عشق است. او به ده سال زندان محکوم شد.
هر چند شلیک یهودی نبود، ولی دلیل قتل را عمدتاً به تب ضد-یهودی که در آن موقع بر
وین حاکم بود نسبت میدهند. از این بدتر، هنگامی که آلمان اتریش را تسخیر
کرد، در حالی که هنوز دو سال از حبس نلبوک باقی مانده بود، او را از زندان آزاد
کردند.
قتل شلیک تاثیر زیادی بر روی گودل گذاشت. او نیز نشانههای پارانویا را از
خودش بروز داده بود. گودل یهودی نبود، ولی بسیاری از دوستانش یهودی بودند. زندگی
تحت رژیم نازی، پارانویا سرانجام دیوانگی بود. او به تشویشی دچار شده بود که انگار
میخواستند او را مسموم کنند، و چند ماه را برای درمان این بیماری ذهنی سپری کرد.
سالها بعد در اواخر عمرش، هنگامی که نشانههایی از بیماری ذهنی و پارانویا در او
ظاهر شد، این ترس دوباره به سراغش آمد. او هیچ غذایی را به غیر آنچه زنش برای او
میپخت نمیخورد. در 1977 همسرش دوبار سکته کرد، و برای مدتی طولانی در بیمارستان
بستری شد، و بنابراین دیگر قادر نبود برای او غذایی بپزد. او از غذا خوردن دست
کشید، و نهایتاً بر اثر گرسنگی فوت کرد. این یکی از غمانگیزترین و پوچترین پایانها
برای یکی از بزرگترین متفکرین قرن بیستم بود.
گودل همان سال به شهروندی اتریش درآمد (هنگام الحاق اتریش به آلمان در 1938،
شهروندی او بصورت خودکار به آلمانی تغییر یافت). او در 1930 دکترای خودش را گرفت.
در 1930 او با انتشار مقالهای تحت عنوان ’درباب گزارههای صوری غیرقابل تصمیمِ
[کتابِ] اصولِ ریاضیات[7]
و دستگاههای مشابه‘ آرزوی هیلبرت را بر باد داد. در این مقاله ثابت شده بود
که هیچ دستگاه اصل موضوعی که آنقدر غنی باشد که ریاضیات را صورت بندی کند نمیتواند
از لحاظ منطقی کامل باشد، و این یعنی غیر ممکن است بتوان اثبات کرد چنین دستگاهی
سازگار است. من کمی بعد درباره کتاب اصولِ ریاضیات برای شما توضیح خواهم
داد. او در 1932 فوق دکترای خودش را گرفت و در 1933 در دانشگاه وین به سمت
استادیاری مشغول شد. در همان سالها بود که حوادث دلخراشی در اروپا درحال رخ دادن
بود. او برای فرار از اتریش نازی به ایالات متحده رفت. و آنجا با اینشتین
ملاقات کرد و با او دوست شد.
او در 1938 با دختری بنام ادل نیمبورسکی که یازده سال پیش او را در وین
در یک کلوپ شبانه ملاقات کرده بود ازدواج کرد. ادل شش سال از او بزرگتر بود، و
قبلاً ازدواج کرده بود. پدر و مادر گودل هر دو با این ازدواج مخالف بودند، ولی او
خاستههای آنها را نادیده گرفت. هنگامی که در 1939 جنگ جهانی دوم آغاز شد، گودل از
این بابت که ممکن است او را از طرف ارتش آلمان به جبهه بفرستند نگران شد. وضعیت بد
سلامتی او باید مانع اعزام او به جنگ میشد، ولی قبلاً او را اشتباهاً بدلیل اینکه
یهودی بودن دستگیر کرده بودند، پس حالا هم احتمال داشت او را بجای یک آدم سالم به
جنگ بفرستند. او تلاش کرد یک ویزای تقلبی برای آمریکا تهیه کند، و از راه
روسیه و ژاپن با همسرش به آمریکا رفت. آنها در 1940 به آنجا رسیدند. در آن سال او
اثبات کرد که فرضیه پیوستار کانتور (Cantor’s
Continuum Hypothesis) با اصول
موضوعه مبتنی بر مجموعهها در ریاضیات سازگار است. او ابتدا بعنوان یک عضو عادی
شغلی را در مرکز مطالعات پیشرفته پرینستون گرفت، که از 1953 به بعد به مقام
استادی ارتقاء یافت. هرچند او از 1946 به بعد کتابی ننوشت، ولی تحقیقات خودش را
ادامه داد.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

آلن متیسون تورینگ (Alan Turing):
تولد: 23 ژوئن 1912، لندن. وفات: 7 ژوئن 1954، لندن.
بر طبق
گفته همکارش جک گود، که در بچلی پارک با آلن تورینگ کار میکرد، او از تب یونجه رنج میبرد.
تورینگ با دوچرخه به دفتر میآمد، و هنگام بهار برای اینکه خودش را از گردهها
محافظت کند، ماسک گاز به صورتش میزد. دوچرخهاش نیز معیوب بود، و هر از چندگاهی
زنجیر آن میافتاد، به همین خاطر تورینگ با خودش یک قوطی روغن، و یک پارچه کهنه
داشت که پس از جا زدن زنجیر دستانش را با آن تمیز میکرد.
او که از جا انداختن زنجیر خسته شده بود، نهایتاً تصمیم گرفت این مشکل را بطور
معقولی حل کند. او شروع کرد تعداد رکابهایی که میزند و پس از آن زنجیر میافتاد
را بشمارد. او پی برد که این تعداد بطور قابل ملاحظهای یک عدد ثابت است. با
مقایسه این عدد با تعداد دندههای چرخ و تعداد اسپوکهای چرخ عقب، او به این
نتیجه رسید که تنها وقتی زنجیر میافتاد که هم زنجیر و هم چرخ در وضعیت خاصی قرار
گرفته باشند. سپس یک مکانیزم شمارنده تعبیه کرد که پیش از اینکه در چنین وضعیتی
قرار گیرد به او هشدار میداد و او میتوانست با یک مانور از این وضعیت جلوگیری
کند. او دیگر نیازی نداشت تا با خودش روغن و پارچه حمل کند. نهایتاً معلوم شد مشکل
به یک اسپوک معیوب مربوط است.
این نشانه پیروزی منطق بود، ولی هر کس دیگری جای او بود دوچرخه را به یک تعمیرگاه
میبرد، جایی که یک تعمیرکار فوراً این مشکل را حل میکرد! از سوی دیگر، با نسپردن
دوچرخه خودش به دست یک تعمیرکار، تورینگ در هزینه تعمیر صرفه جویی کرد. مانند
بسیاری چیزهای دیگر، او همیشه دلایلی برای کارهای خودش داشت، و فقط روالش با بقیه
فرق داشت.
![]()
پدر آلن تورینگ، که جولیوس نام داشت، عضو اداره خدمات مدنی هند بود.
مادرش، اتل، دختر یک مهندس راهآهن مَدرَس بود بود. این زوج میخواستند بچههایشان
در انگلستان متولد شوند، بنابراین به لندن نقل مکان کردند. آلن پسر دوم آنها بود.
او هنگامی که شش سال داشت به مدرسه سنتلئونارد رفت، و در آنجا بود که مدیر
مدرسه فوراً فهمید که او استعداد زیادی دارد.
هنگامی که او 13 سال داشت به مدرسه شربورن رفت، یک مدرسه نیمه خصوصی که
محل تحصیل ثروتمندان بود. مانند بیشتر این مدارس، در آنجا نیز بر روی ادبیات
کلاسیک تکیه میشد. دستخط تورینگ بد بود، و ادبیات انگلیسی او نیز خوب نبود، و
حتی در رشته مورد علاقهاش که ریاضیات بود نیز ترجیح میداد به روش خودش کار کند.
با اینحال او کلیه جوایزِ ریاضی مدرسه را میبرد. او شیمی را نیز دوست داشت، ولی
اینجا هم به روش خودش کار میکرد. مدیر مدرسه در جایی نوشته بود که : ’اگر قرار
است او صرفا یک متخصص علوم شود، دارد وقت خودش را در یک مدرسه عمومی تلف میکند.‘
و این کاملاً حقیقت داشت.
اولیای مدرسه نمیدانستند که تورینگ در وقتِ آزادش مقالات انیشتین در مورد
نسبیت، و کتاب ’سرشتِ جهان فیزیکی‘ نوشته آرتور ادینگتون درباره
نظریه کوانتوم را مطالعه میکرد. در 1928 او با کریستوفر مورکوم که یک سال
از او جلوتر بود، دوستی نزدیکی را آغاز کرد. آنها علاقه زیادی نسبت به علم داشتند.
ولی دو سال بعد مورکوم فوت شد. بر اثر این واقعه تورینگ بسیار غمگین شد، ولی با
تلاشی که از خودش نشان داد در کینگزکالجِ کمبریج جایی برای تحصیل برای خودش باز
کرد. او مطالعه کتابهای پیشرفته را ادامه داد، و در سال 1934 فارغالتحصیل شد.
تورینگ خیلی بد لباس بود. حتی وقتی هم کت و شلوار میپوشید، به ندرت اتو کشیده
بود. خندههایش بلند و حالتی عرعر مانند داشت. او در حرف زدن ایراد داشت. تورینگ
در اصلاح صورتش تنبل بود و غالباً ته ریش نازکی داشت. خیلی جاها او را بعنوان یک
آدم عصبی که از نظر اجتماعی بیعرضه بود معرفی میکردند، ولی در واقع او خیلی
محبوب و خوش برخورد بود. رفتارهای به ظاهر غیر عادی او از این نشئت نمیگرفت که او
درباره چه چیزی میاندیشد، بلکه بیشتر از چگونگی فکر کردن او ناشی میشد.
هنگامی که تورینگ بر روی مسئلهای کار میکرد، زوایایی را پیدا میکرد که هیچ کس
نمیدانست وجود دارند.
یک سال بعد او زیر نظر ماکس نیومان (Max Newman) مشغول
گذراندن دوره فوق لیسانسش در حوزه مبانی ریاضیات بود. در آن موقع او با برنامه
هیلبرت و ابطال آن توسط گودل آشنا شد. تورینگ متوجه شد که قضیه تصمیمناپذیری گودل
درواقع درباره الگوریتمها (algorithms) است. یک سئوال
درصورتی تصمیمپذیر است که برای جواب دادن به آن الگوریتمی وجود داشته باشد. با
یافتن یک الگوریتم برای یک مسئله مفروض، شما میتوانید آن را اثبات کنید. از سوی
دیگر تصمیمناپذیری ژرفتر و دشوارتر است، زیرا شما باید اثبات کنید چنین
الگوریتمی وجود ندارد. تلاش برای اثبات چنین چیزی مایوسکننده است، مگر اینکه شما
تعریف دقیقی از یک الگوریتم داشته باشید. درواقع گودل با در نظر گرفتن یک الگوریتم
بعنوان یک اثبات در درون یک دستگاه اصل موضوعه با این موضوع برخورد میکرد. در عوض
تورینگ شروع به فکر کردن درباره فرمولبندی الگوریتمها بصورت کلی کرد.
![]()
او در سال 1935 بخاطر کشفیات مستقلی که درباره قضیه حد مرکزی (central limit theorem) در احتمالات انجام داد به عضویت هیئت علمی دانشگاه کینگزکالج
درآمد. این قضیه پایههای منطقی برای کاربرد گسترده از منحنی زنگولهای (bell curve) یا
توزیع
نرمال را در استنتاج آماری فراهم میآورد. ولی در سال 1936 بود که او با انتشار
مقاله مهم خودش با نام ’درباب اعداد قابلمحاسبه، با کاربردهایی در مسئله تصمیم‘
قدم در راه قضایای گودل گذاشت. در این مقاله او یک قضیه تصمیمناپذیر درباره یک
مدل صوری محاسبه، که حالا ماشین تورینگ (Turing machine) نامیده میشود،
را اثبات کرد. او اثبات کرد که هیچ الگوریتمی نمیتواند از پیش تصمیم بگیرد که آیا
یک محاسبه با یک جواب متوقف میشود یا نه. اثبات او از گودل سادهتر است، هرچند هر
دو آنها برای فراهم آوردن زمینه مورد نظر به ترفندهای ابتدایی نیاز دارند.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

بنوآ ب. مندلبرو (Benoit Mandelbrot):
تولد: 20 نوامبر 1924، لهستان. وفات: 14 اکتبر 2010، آمریکا.
به علت
اختلالی که جنگ جهانی دوم پدید آورده بود، ورودی دو دانشگاه مهم پاریس، یعنی اکولنرمال و
مدرسه پلیتکنیک، شش ماه به تاخیر افتاد. امتحانات یک ماه به طول کشید و
بسیار دشوار بودند، ولی بنوآی جوان در هر دو آنها قبول شد. یکی
از معلمان متوجه شد که در میان همه داوطلبان کنکور تنها یک نفر توانسته به یک
سئوال مشکل ریاضی پاسخ دهد. او حدس زد که این شخص باید مندلبرو باشد، و با پرس و
جویی که انجام داد فهمید که درست حدس زده. معلم اعتراف کرده بود که ’بدلیل وجود یک
انتگرال سهگانه وحشتناک که در قلب این مسئله قرار داشت‘، حل آن برای خودش نیز غیر
ممکن بوده.
مندلبرو وقتی این را شنید گفت ’خیلی ساده بود‘، و سپس شرح داد که آن انتگرال
یک مسئله انحرافی بود، و در واقع حجم یک کره را نشان میداد. اگر شما از دستگاه
مختصات مناسبی استفاده کنید، چنین چیزی واضح بود، و همه نیز فرمول حجم یک کره را
میدانند. همه چیزی که در مورد این مسئله به ظاهر سخت وجود داشت همین بود. هنگامی
که شما متوجه ترفند شوید، میفهمید که حق با مندلبرو بود. معلم که شوکه شده بود
مِن مِن کنان گفت ’البته، البته!‘ ولی چرا خودش متوجه آن نشده بود؟
زیر او به شکل جبری فکر میکرد، نه به شکل هندسی.
مندلبرو ذاتاً یک هندسهدان بود، با یک بینش قوی بصری. بعنوان یک یهودی که در
فرانسه اشغالی زندگی میکرد، همیشه این خطر وجود داشت که توسط نازیها دستگیر شود
و سر از اردوگاههای مرگ درآورد. ولی پس از پشت سرگذاشتن این دوران کودکی سخت، او
به آمریکا رفت و در آزمایشگاههای توماس واتسون به استخدام شرکت IBM درآمد. در آنجا او یک سری مقالات را
منتشر کرد که در زمینههای مختلفی بودند، از تناوب لغات در زبانها گرفته تا سطح
سیل در رودخانهها. سپس با یک سری الهاماتی که به وی دست داد، او همه این تحقیقات
مختلف و متنوع را در یک مفهوم هندسی واحد خلاصه کرد، چیزی که حالا فراکتال (fractal)
نامیده میشود.
اشکال عادی هندسه، مثل کره، مخروط، یا استوانه، شکل بسیار سادهای دارند. هر
چه قدر از نزدیک به آنها نگاه کنید، میبینید که چقدر هموارتر و مسطحتر بنظر میرسند.
جزئیات کلی ناپدید میشوند، و آنچه میماند بیشتر شبیه یک صفحه بیشکل است. ولی
فراکتالها متفاوتند. در هر مقیاسی، و هر چقدر هم که یک فراکتال را بزرگ کنیم،
دارای ساختار پرجزئیاتی است. آنها بطور بینهایتی پرپیچ و خم هستند. مندلبرو مینویسد:
’ابرها کروی شکل نیستند، کوهها مخروطی نیستند، سواحل دریا دایرهشکل نیستند، پوست
درختان هم صاف نیست، همینطور رعد و برق نیز در خط مستقیم حرکت نمیکند.‘ فراکتالها
جنبههایی از طبیعت را نشان میدهند که ساختارهای متداول فیزیکِ ریاضی نمیتوانند
اینکار را انجام دهند. آنها در چگونگی مدلسازی دانشمندان از جهان واقعی تغییرات
بنیادی پدید آوردند. فراکتالها در فیزیک، نجوم، زیستشناسی، زمینشناسی، زبانشناسی،
بازارهای مالی جهانی، و بسیاری از حوزهها دیگر کاربرد دارند. آنها همچنین دارای
ویژگیهای خالص ریاضی هستند، و با دینامیکِ آشوب پیوندهای قوی دارند.
فراکتالها یکی از چندین حوزههای ریاضی هستند، که هرچند خیلی جدید نیستند،
ولی در نیمه دوم قرن بیستم اوج گرفتند، و با فراهم آوردن روشها و دیدگاههای
جدید، رابطه میان ریاضیات و کاربردهای آن را تغییر دادند. ریشههای هندسه
فراکتال به تلاشهایی باز میکردد که برای یافتن دقت در آنالیز در آواخر قرن
نوزدهم انجام شده بود، و به اختراع ’منحنیهای غیرعادی‘ (pathological curves)
انجامید، که نقش اصلی آنها این بود که نشان دهند استدلالاتِ شهودیِ عادی چقدر میتوانند
اشتباه باشند. برای نمونه، هیلبرت یک منحی را تعریف کرد که از تمام نقاط داخل یک
مربع عبور میکرد (یعنی نه فقط از نزدیک آنها، بلکه دقیقاً به همه آنها برخورد میکرد).
به دلایل واضح، چنین چیزی یک منحنی فضا-پرکن نامیده میشود، و ما را وامیدارد
تا با احتیاط بیشتری درباره مفهوم بُعد فکر کنیم. در اینجا یک تبدیل پیوسته میتواند
بُعد فضا را از 1 به 2 افزایش دهد. نوع دیگری از اینها ’منحنی دانهبرفی هلژ فون کوخ‘ (Helge von Koch’s snowflake curve) است، که طول بینهایتی دارد، ولی یک مساحت متناهی را محصور میکند،
و همچنین مثلث شرپینسکی (Sierpiński’s
gasket)، که یک منحنی است که از کلیه نقاط
خودش عبور میکند.
ولی صرف نظر از حوزههای خاص، موارد ذکر شده اهمیت زیادی نداشتند، و فقط
بعنوان کنجکاویهای منفرد درنظر گرفته میشدند. به منظور اینکه یک حوزه اهمیت پیدا
کند، کسی باید پیدا شود که اجزاء آن را درکنار یکدیگر قرار دهد، آنها را تحت یک
موضوع واحد باهم متحد کند، مفاهیم لازم را بصورتی کلی فرمولبندی کند، و سپس تلاش
کند این ایده را به بقیه بقبولاند. مندلبرو، که از لحاظ سنتی یک ریاضیدان معمولی
نبود، فقط یک بصیرت داشت و با سرسختی تلاش کرد آن را به جهان عرضه کند.
![]()
بنوآ در یک خانواد یهودی لیتوانیایی زاده شد که بیشتر آنها دانشگاهی بودند.
مادرش بلا، یک دندانپزشک بود. پدرش کارل، که هیچ تحصیلات دانشگاهی
نداشت، تولید کننده و فروشنده لباس بود، ولی بیشتر افراد خانواده آنها برای چنین
نسل همه اشخاص تحصیل کرده بودند، بنابراین بنوآ در یک خانواده دانشگاهی پرورش
یافت. پدرش یک برادر کوچک بنام سولم داشت که بعدها یک ریاضیدان برجسته شد.
مادرش بواسطه یک بیماری همهگیر یکی از بچههایش را از دست داده بود، و چون
میخواست از ابتلاء بنوآ جلوگیری کند، برای چند سال او را از رفتن به مدرسه دور
نگاه داشت. یکی از عموهای دیگرش بنام لوترمان در خانه به او آموزش میداد،
ولی او معلم خیلی خوبی نبود. بنوآ یاد گرفت چگونه شطرنج بازی کند، و به داستانها
و اسطورههای کلاسیک گوش میداد، ولی کار دیگری انجام نمیداد. ولی او توانایی
فکر کردنِ بصری را در خودش پرورش داد. حرکات او در بازی شطرنج بیشتر بواسطه شکلِ
بازی انجام میشد – بعبارتی، الگوی مهرهها چیده شده بر روی صفحه. او به نقشهها علاقه داشت،
تمایلی اکه احتمالاً از پدرش، که یک کلکسیونر نقشه بود، به ارث برده بود. این نقشهها
روی دیوارهای خانه آنها آویزان بودند. او همچنین هر چه را به دستش میرسید میخواند.
در 1936 خانواده آنها بعنوان پناهنده اقتصادی و سیاسی لهستان را ترک کردند.
مادرش نمیتوانست بعنوان پزشک به کارش ادامه دهد و پدرش هم ورشکسته شده بود. آنها
به پاریس، که خواهر پدرش در آنجا زندگی میکرد، رفتند. بعداً مندلبرو تعریف میکرد
که همین زن بود که زندگی آنها را نجات داد و کمک کرد تا از افسردگی دور بمانند.
عموی بنوآ، سولم مندلبر (Szolem Mandebrojt)، کمکم
داشت در جهان ریاضیات اسم و رسمی پیدا میکرد و هنگامی که سولم استاد دانشگاه
کلرمونت-فراند شد، بنوآ تنها پنج سال داشت. هشت سال بعد او به سمت استاد کالج دو
فرانس در پاریس برگزیده شد. بنوآ که تحت تاثیر موفقیتهای عمویش قرار گرفته
بود کمکم با خودش فکر میکرد که خودش هم به ریاضیات وارد شود، هر چند پدرش با این
مخالف بود و آن را کار بیفایدهای میدید.
هنگامی که مندلبرو در دوران نوجوانی بود، سولم مسئولیت تحصیلات او را به عهده
گرفت. او در پاریس به لیسه رولین رفت. ولی فرانسه اشغالی برای یهودیان جای
بدی بود، و او دوران کودکی با فقر و تهدید دائمی روبرو بود. در 1940 بار دیگر
خانواده آنها کوچ کردند، و اینبار به جنوب فرانسه رفتند، جایی که عمویش یک خانه
ییلاقی داشت. پس از آن نازیها جنوب فرانسه را نیز اشغال کردند و مندلبرو حدود یک
سال و نیم در حال فرار بود. او این دوره از زندگی خودش را با جملات غمانگیزی
توصیف میکند:
برای چندین ماه من بعنوان یک کارگر راهآهن کار میکردم. اینکار بهتر از کار
متداول آن زمان، یعنی تیمارکردن اسبها بود، ولی من نه شبیه یک کارگر و نه مثل یک
تیمار کننده اسب بودم و مانند آنها هم حرف نمیزدم. به همین دلیل نزدیک بود یکبار
اعدام یا اخراج شوم. برخی از دوستانم نهایتاً توانستند وارد کالج لیسه دو پارک
در لیون شوند. درحالی که بیشتر دنیا در آشوب بود، ولی دغدغه اصلی در آن جا
کنکور بود. چند ماهی را که در لیون سپری کردم از مهمترین دورانهای زندگیم محسوب
میشوند. فقر و ترس شدید از حکمران آلمانی شهر، که بعداً معلوم شد کلاوس باربی (Klaus
Barbie) است، بیشتر اوقات مرا پشت میزم
چسبانده بود.
باربی یکی از بدنامترین افسران (SS) و گشتاپو بود. او بدلیل شکنجه و کشتار زندانیان بعنوان قصاب لیون
شناخته میشد. بعد از جنگ او به بولیوی گریخت، ولی در سال 1983 به دلیل جنایت
علیه بشریت به فرانسه مسترد و تا آخر عمرش (1991) در زندان بود.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.

ویلیام تورستون (William Thurston):
تولد: 30 اکتبر 1946، آمریکا. وفات: 21 آگوست 2012، آمریکا.
ریاضیدانان
هیچ چیز را به اندازه حرف زدن درمورد ریاضیادانانِ دیگر دوست ندارند (مخصوصاً در مورد
کارهای آنها)، و اینکار را به امید این انجام میدهند تا ایدههای جدیدی را کسب
کنند که در مسائلی که با آن روبرو هستند به آنها کمک کند. آنها همچنین دوست دارند
تا درباره چیزهایی مثل رستوران جدیدی که گوشه دانشگاه باز شده، و درباره خانواده و
دوستان مشترکشان صحبت کنند. آنها معمولاً اینکار را در هنگامی که در گروههای
کوچکی مشغول نوشیدن قهوه یا چای هستند انجام میدهند. همانطور که ریاضیدان
مجارستانی آلفرد رنیی زمانی گفته بود ’یک ریاضیدان ماشینی است که قهوه را به
قضایای ریاضی تبدیل میکند!‘ در زبان آلمانی نیز لغت Satz هم به معنی قضیه، و هم به معنی ’دانههای قهوه‘ است.
معمولاً این جور گفتگوها بیشتر در سمینارهای رسمی (سخنرانیهای فنی برای
متخصصین)، کنفرانسها (سخنرانیهایی که کمتر فنی هستند و برای متخصصین یا
دانشجویان فارغالتحصیلی که در حوزههای دیگری کار میکنند)، کارگاهها (یک
کنفرانس نسبتاً کوچک)، و یا کنفرانسهای بزرگ صورت میگیرد. در دسامبر 1971
دانشگاه کالیفرنیا در برکلی میزبان سمیناری درباره دستگاههای دینامیکی بود. بدلیل
کارهایی که استفن اسمیل (Stephen
Smale)، ولادیمیر آرنولد (Vladimir Arnold) و
همکارانشان در برکلی و مسکو در مورد نظریه آشوب کرده بودند، به تازگی دستگاههای
دینامیکی به موضوع جذابی تبدیل شده بود. یک دستگاه دینامیکی (dynamical system) هر
چیزی است که بر اساس قواعد غیر-تصادفی (non-random) در طول
زمان شکل میگیرد. برای یک دستگاه دینامیکی پیوسته، قواعد معادلات دیفرانسیلی
هستند که وضعیت آن را در لحظه بسیار کوچکی در آینده به شکل جملاتی از وضعیت کنونی
دستگاه مشخص میکنند. مفهوم مشابهای از یک دستگاه دینامیکی گسسته (discrete)
وجود دارد که در آن زمان بصورت لحضات مجزا (1، 2، 3،
...) سپری میشود. سخنران سمینار کشف مهمی را در رابطه با مسئله توضیح میداد که
به استفاده از تعداد متناهی از نقاط در صفحه خلاصه میشد. سخنران یک ترفند
مهم را شرح میداد، و آن این بود که چگونه هر تعداد مفروضی از نقاط را به مکانهای
جدیدِ نه چندان دور منتقل کرد، بصورتی که آنها در هر مرحله از حرکت زیاد سرگردان
نمانند (چند شرط دیگر نیز باید برقرار باشد). اثبات این قضیه برای فضاهای سه یا
بیشتر آسان بود، ولی حالا اثباتی برای دو بعد ارائه میشد که خیلی وقت بود
ریاضیدانان به دنبال آن بودند. این قضیه اثرات بسیار جالبی بر روی دستگاههای
دینامیکی داشت.
در ته سالن دانشجوی کمرویی نشسته بود که به تازگی فارغالتحصیل شده بود.
قیافه او با ریش و موهای بلندی که داشت شبیه هیپیها بود. او بلند شد و با خجالت
گفت که فکر نمیکند این اثبات صحیح باشد. او به سمت تختهسیاه رفت و دو تصویر کشید
کرد، که هرکدام نشان دهند هفت نقطه در صفحه بودند، و با استفاده از روشهایی که در
سخنرانی مطرح شده بود شروع به حرکت دادن نقاط شکل اول به شکل دوم کرد. او مسیرهایی
را رسم کرد که قرار بود نقاط در طول آنها حرکت کنند، و آنها شروع کردند تا سر راه
یکدیگر قرار گیرند، و برای جلوگیری از مانع لازم بود مسیر بعدی راه بیشتری را
بپیماید، که به نوبه خودش باعث میشد مانع طولانیتری بوجود آید. همانطور که منحنیها
مانند سرهای هیدرا[8]
جوانه میزدند، مشخص شد که این دانشجو درست میگوید. دنیس سالیوان (Dennis Sullivan) که
در آن سمینار حضور داشت بعداً گفت ’من هیچ وقت تا به حال چنین مثال نقیضی ندیده
بودم که به چنین شکل خلاقانهای و اینقدر سریع بیان شود.‘
این دانشجو ویلیام تورستون بود، که دوستان و همکارانش او را
’بیل‘ صدا میزدند. داستانهای مشابه زیادی در مورد او وجود دارند. او یک بینش
ذاتی برای هندسه داشت، به ویژه وقتی اوضاع واقعاً پیچیده میشد، هندسههای
چندبُعدی (چهار، پنج، شش ...) که تازه توسعهیافته بودند، برای او قلمروهای وسیعی
را فراهم میآوردند تا مسائل فنی را به نسخه تجسمی تبدیل کرده، و سپس آنها را حل
کند. او استعداد عجیبی برای دیدن پیچیدگی و کشف اصول ساده داشت. او یکی از
توپولوژیدانان پیشتاز دوران خودش بود، که بسیاری از مسائل مهم این حوزه را حل
کرد، و چند حدس کلیدی را مطرح کرد که حتی با همه استعدادِ نبوغآمیزی که داشت
نتوانست آنها را اثبات کند. بیل تورستون یک شخصیت برجسته ریاضیاتِ محض است،
که به واقع نماینده ریاضیدانان نابغه دوران خودش بود.
![]()
کنایهآمیز این بود که باوجود ادراکِ بصری بسیار خوب تورستون، بینایی او ضعیف
بود. چشمان او بصورت مادرزادی کج بودند، و نمیتوانست هر دو چشمش را روی اشیاء
نزدیک متمرکز کند. این بر روی ادراک او از عمق تاثیر گذاشت، طوری که تجسم
اجسام سه-بُعدی از روی اجسام دو-بعدی برای او مشکل بود. مادرش که مارگارت
نام داشت، خیاط بسیار ماهری بود که میتوانست الگوهایی را بدوزد که آنقدر پیچیده
بودند که نه بیل و نه پدرش پُل میتوانستند آنها را درک کنند. پل یک مهندسِ
فیزیکدان بود که در آزمایشگاههای بل کار میکرد و علاقه شدیدی به درست کردن
ابزارکها داشت. او یکبار به بیل یاد داده بود که چطور با دست خالی آب را جوش
بیاورد (ابتدا از یک پمپ خلاء برای کاهش نقطه جوش آب استفاده کرد، طوری که نقطه
جوش کمی بالاتر از دمای اطاق باشد؛ سپس با مالش دستهای خودتان به ظرف میتوانید
آن را گرم کنید.) هنگامی که بیل دو سال داشت، مادرش برای کمک به کجبینی او ساعتها
در کنار او مینشست و کتابهایی را به او نشان میداد که پر از الگوهای رنگی
بودند. علاقه آتی او به الگوها، و تبدیل شدن به یک تعمیرکار ماهر، احتمالاً از
همین فعالیتها سرچشمه گرفته بود.
دوران تحصیل او غیرمتعارف بود. دبیرستانی که در آن درس میخواند بسیار خاص بود
و تنها به دانشآموزان معدودی اجازه ورود میداد که از تواناییهای بالایی
برخوردار بودند. دوران دانشجویی او در دانشگاه برکلی منظمتر بود، ولی با اعتراضات
دائمی دانشجویان به جنگ ویتنام، آن موقع هم دوران متلاطمی بود. تورستون به کمیتهای
ملحق شد که سعی داشت ریاضیدانان را قانع کند که سرمایهگذاریهای تحقیقاتی نظامی
را قبول نکنند. در آن موقع او با ریچل فیندلی ازدواج کرده بود و اولین بچه
آنها نیز بدنیا آمده بود. ریچل میگفت بخشی از تلاشهایم این بود که مطمئن شوم
تورستون به استخدام ارتش درنیاید. اینکارها با زمان امتحانات دکترای تورستون
همزمان شده بود، و عملکرد او غیرعادی، ولی مثل همیشه اصیل بود. رساله دکترای او در
مورد مسائل خاصی بود که برگبرگ شدن (foliations) نامیده میشود،
و در آن یک مانیفلد (manifold)، یا به عبارتی یک فضای چندبُعدی، به برگههایی تجزیه میشوند،
مانند صفحات یک کتاب، ولی چیدمان آن نسبت به کتاب از نظم کمتری برخوردار است. این
مبحث به رویکرد توپولوژیک به دستگاههای دینامیکی مربوط است. رساله او حاوی چند
نتیجه مهم بود، ولی هیچ وقت چاپ نشد. برگبرگ شدن اولین حوزه تحقیقاتی عمده
تورستون بود، و او تحقیق درمورد آنها را طی سالهای 73-1972در موسسه مطالعات پیشرفته
پرینستون، و 74-1973 در دانشگاه MIT
ادامه داد. تا آنجا که به ریاضیدانان دیگر مربوط است، او حقیقتاً بسیاری از مسائل
اصلی این مبحث را حل کرد، و نهایتاً آن را بکلی به اتمام رساند.
![]()
در 1974 تورستون استاد دانشگاه پرینستون شد (که نباید آن را با مرکز مطالعات
عالی اشتباه گرفت، که دانشجو ندارد و صرفاً یک مرکز تحقیقاتی است). چند سال بعد
تحقیقات او به سمت یکی از دشوارترین حوزههای توپولوژی، یعنی مانیفلدهای سه-بعدی،
معطوف شد. این فضاها مشابه سطوح هستند، ولی یک بعد اضافی دارند. مطالعه آنها به
حدود یک قرن قبل و پوانکاره بازمیگردد، ولی تا وقتی تورستون درگیر نشده بود،
همیشه آنها گیجکننده بنظر میرسدند. توپولوژی مانیفلدهای ابعاد-بالا غیر عادی
است. سادهترین ابعاد عبارتند از بُعد 1 (ساده) و 2 (سطوحی که بصورت کلاسیک حلشدهاند).
معلوم شد که سادهترین حالت بعدی 3 نیست، بلکه 5 یا بالاتر است، زیرا فضاهایی که
ابعاد بالاتری دارند جای فراوانی برای مانورهای پیچیده دارند. حتی در آن ابعاد نیز
مسائل دشوار هستند. هنوز مسائل سخت به مانیفلدهای 4-بُعدی، و سختترین آنها به
مانیفلدهای 3-بُعدی مربوطند، زیرا آنها بهاندازه کافی جا برای پیچیدگی دارند، و
نه اینکه به اندازه کافی به طریق آسانی برای ساده شدن جا داشته باشند.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.
ما از
شخصیتهای برجسته خودمان، که کشفیاتِ راهگشای آنها چشماندازهای جدیدی را در
ریاضیات گشود، چه چیزی آموختیم؟
آشکارترین پیام در تنوع ریاضیات است. پیشگامان ریاضی از همه دورانهای تاریخ،
از همه فرهنگها، و از همه طبقات آمدهاند. داستانهایی که من در اینجا بازگو کردهام
یک بازه تاریخی 2500 ساله را شامل میشود، که قهرمانان آن در یونان، چین، ایران،
هند، ایتالیا، فرانسه، سوئیس، آلمان، روسیه، انگلستان، ایرلند، و آمریکا زندگی میکردند.
برخی از آنها، مثل فرما، کینگ، و کووالوسکایا، در خانوادههای ثروتمندی بدنیا آمده
بودند. برخی از طبقات متوسط بودند، و برخی هم، مانند گاوس و رامانوجان، در خانوادههای
فقیری بدنیا آمدند. برخی مثل کاردانو و مندلبرو، از خانوادههای اهل علم آمدند.
برخی مانند اویلر، فوریه، گالوا، گودل، و تورینگ، در دوران سختی زندگی میکردند.
برخی هم، مانند مادهاوا، فرما، نیوتون، و تورستون، این شانس را داشتند تا در
جوامعه باثباتتری زندگی کنند. برخی از آنها، مثل فوریه، گالوا، و کاوالوسکایا،
هم فعالیت سیاسی داشتند، که از میان اینها دو نفر اول به همین خاطر به زندان
رفتند. برخی هم، مانند اویلر و گاوس، سیاست را پیش خودشان نگاه داشتند.
...........................................
برای ادامه مطالعه این فصل
نسخه کامل PDF
کتاب را تهیه کنید.
[1] - نشانههایی که برای طالعبینی بر روی استخوانها حک میشدند.
[2] - در برخی از کتابهای فارسی نام نیوتون را آیزاک، و
اسحاق نیز آوردهاند، ولی تلفظ صحیح انگلیسی آن آیزِک است (مترجم).
[3] - یک قمار خطرناک، که شبیه خودکشی است و تنها با گذاشتن یک
گلوله در هفت تیر و خالی کردن آن به مغز انجام میشود. در اینحالت، احتمالِ مرگِ
شخص به میزان یک به هفت است (مترجم).
[4] - در الهیات مسیحی تثلیث مقدس عبارت است از اتحاد
پدر، پسر (عیسی مسیح) و روحالقدس در خدای واحد (مترجم).
[5] - فیودور داستایفسکی )
Fedor Dostoievski ) 1881-1821 نویسنده بزرگ روسی قرن
نوزدهم (مترجم).
[6] - ساری لباسی است که زنان هندی به تن میکنند
(مترجم).
[7] - کتاب اصول ریاضیات (Principia Mathematica) تالیف وایتهد و راسل (مترجم).
[8] - در افسانههای یونانی هیدرا (hydra) یک مار 9 سر بود که بدست هرکول کشته شد (مترجم).